B-Splines/de

Diese Seite beschreibt, wie man B-Splines in FreeCAD verwendet. Sie gibt auch Hintergrundinformationen, was B-Splines sind und für welche Anwendungen sie nützlich sind.

Motivation

Wenn du bereits über B-Splines und deren Anwendung Bescheid weisst, kannst du direkt mit dem Abschnitt B-Splines in FreeCAD fortfahren.

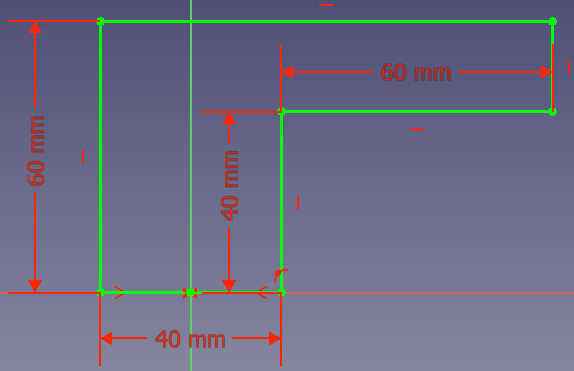
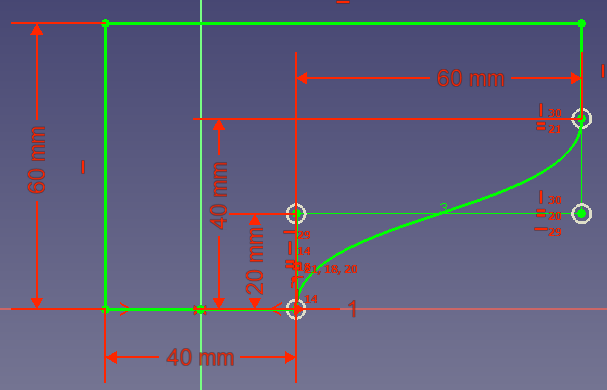
Nehmen wir an, Du willst ein Teil entwerfen, das mit einem 3D Drucker hergestellt werden soll. Das Teil muss so eine Kante haben:

Du musst das Teil in Richtung der Unterseite der Skizze nach oben drucken. Äußere Stützstrukturen sind möglicherweise keine Option. Daher musst Du eine Stütze direkt an deinem Teil anbringen. Welche Möglichkeiten hast du?

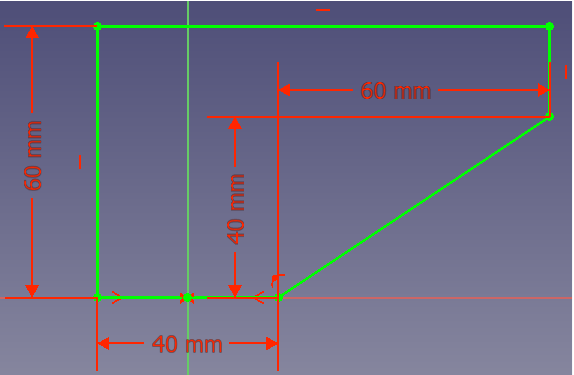
Option 1: du kannst eine Linie vom Punkt (20, 0) zum Punkt (80, 40) hinzufügen:

Allerdings benötigt diese Lösung viel Volumen, also Gewicht und Material.

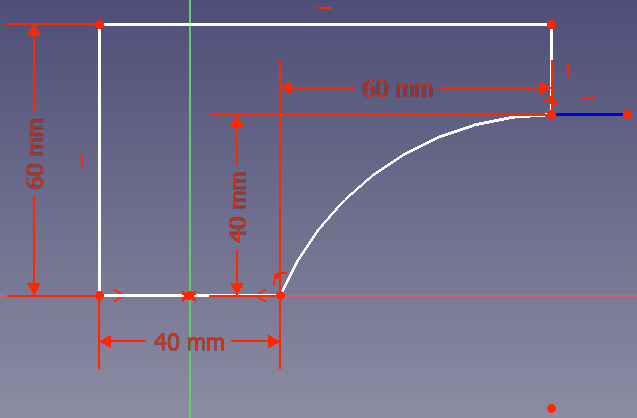
Option 2: du kannst die beiden Punkte mit einem Kreisbogen verbinden. Um Volumen zu sparen, sollte der Bogen tangential im Punkt (80,40) enden. Dann sieht deine Lösung wie folgt aus:

GUT. Aber ganz unten brauchst du keine sofortige Unterstützung.

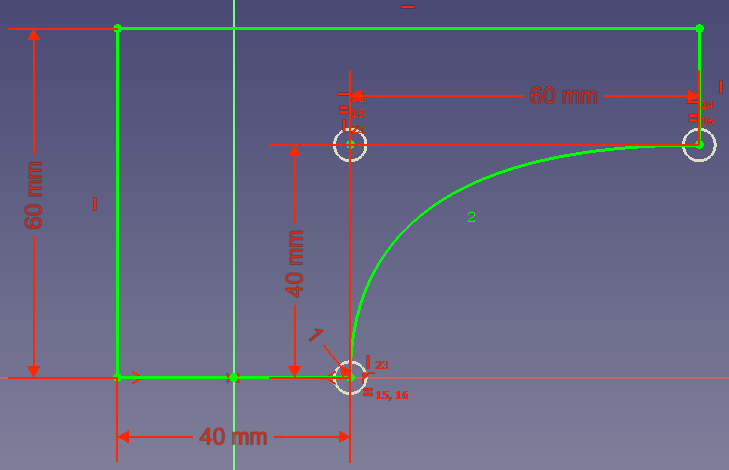
Option 3: du kannst noch mehr Volumen einsparen, wenn die Verbindung zwischen den beiden Punkten eine Kurve wäre, die tangential bei (0, 20) beginnt und tangential bei (80, 40) endet:

So kann eine Kurve, mit der du zwei Punkte tangential zu einem Bezugspunkt verbinden kannst, sehr nützlich für Konstruktionen sein. Bézierkurven bieten diese Möglichkeit.

Bézierkurven

Herleitung

Bézierkurven sind Polynome zur Beschreibung der Verbindung zwischen 2 Punkten. Das einfachste Polynom, das 2 Punkte verbindet, ist eine Gerade ( $A * x^{1} + B$ ), also sind lineare Bézierkurven auch Strecken (Geradenabschnitte):

Animation 1: Lineare Bézierkurve.

Ein Polynom wird jedoch erst dann nützlich, wenn wir es steuern können. Es sollte also einen Punkt zwischen den beiden Endpunkten geben, der es uns erlaubt festzulegen, wie die Endpunkte verbunden werden. Wie unter Option 3 im Beispiel oben, ist die Kurve hilfreich, wenn sie tangential zu Linien beginnt und endet, die über die Endpunkte verlaufen. Und das ist ein Hauptmerkmal von Bézierkurven. Fügen wir also einen Kontrollpunkt zwischen den 2 Endpunkten ein. Die Kurve beginnt tangential, auf diesem Kontrollpunkt zulaufend, d. h. sie ist tangential zu der Linie, die wir zwischen dem Startpunkt und dem Kontrollpunkt ziehen können. Wenn man vom Endpunkt aus rückwärts geht, ist die Kurve ebenfalls tangential zu der Linie, die wir zwischen dem Kontrollpunkt und dem Endpunkt zeichnen können. Animation 2 zeigt, wie eine solche Kurve aussieht.

Animation 2: Quadratische Bézierkurve. P1 ist hierbei der Kontrollpunkt.

Die Animation verdeutlicht, worum es sich bei der Kurve im Grunde handelt - um einen Übergang von P0 zu P2, indem die Linie P0-P1 in die Linie P1-P2 gedreht wird. Dadurch erhalten wir das schöne tangentiale Anfang/Ende Merkmal.

Eine solche Kurve kann nur durch ein quadratisches Polynom beschrieben werden. (Die Anzahl der Links-/Rechtsdrehungen + 1 ist die erforderliche Polynomordnung. Ein quadratisches Polynom hat eine einzige Windung, ein kubisches Polynom hat zwei Windungen usw.) Daher ist eine Bézierkurve mit einem Kontrollpunkt eine quadratische Bézierkurve (zweiter Ordnung).

Ein einziger Kontrollpunkt ist oft nicht ausreichend. Nimm das obige Motivationsbeispiel. Bei der Option 3 endet die Kurve tangential in x-Richtung. Aber wie kann man die Punkte (20, 0) und (80, 40) so verbinden, dass die Kurve tangential in y-Richtung endet? Dazu braucht man erst eine Rechts- und dann eine Linkskurve, also ein kubisches Polynom (dritter Ordnung). Und das bedeutet für eine Bézierkurve, dass wir einen zweiten Kontrollpunkt brauchen (oder man kann sagen, wir gewinnen). Animation 3 zeigt eine kubische Bézierkurve.

Animation 3: Kubische Bézierkurve.

Um die Frage zu beantworten: Die Lösung mit dem tangentialen Ende in y-Richtung für das Beispiel ist diese:

Regeln

Im der Herleitung sind vielleicht schon einige "Regeln" für Bézierkurven aufgefallen:

Der Polynomgrad ist auch der Grad der Kurven.
Werden $n$ Krümmungen benötigt, muss die Bézierkurve mindestens vom Grad $n + 1$ sein.
Eine Bézierkurve beginnt immer tangential zu der Linie zwischen dem Startpunkt und dem ersten Kontrollpunkt (und endet tangential zu der Linie zwischen dem letzten Kontrollpunkt und dem Endpunkt).

Mathematik

Wenn du an den mathematischen Hintergründen interessiert bist, hier sind die Grundlagen.

Eine Bézierkurve wird mit dieser Formel berechnet:

$Bezier (n, t) = \sum_{i = 0}^{n} \underset{Polynomausdruck}{\underset{⏟}{(\binom{n}{i})}} \underset{Polynomausdruck}{\underset{⏟}{{(1 - t)}^{n - i} t^{i}}} \underset{Punktkoordinate}{\underset{⏟}{P_{i}}}$

Dabei ist n der Grad der Kurve. Eine Bézierkurve vom Grad n ist also ein Polygon der Ordnung n. Die Faktoren $P_{i}$ sind dabei die Koordinaten der Kontrollpunkte der Bézierkurven. Zur Veranschaulichung siehe Steuerung von Bézierkurven.

Wenn du weiter interessiert bist, sieh dir Die Mathematik der Bézierkurven mit einer schön animierten Herleitung der Mathematik der Bézierkurven an.

B-Splines

Grundlagen

Dieses Video listet zu Beginn die praktischen Probleme mit Bézierkurven auf. Zum Beispiel, dass das Hinzufügen oder Ändern eines Kontrollpunktes die gesamte Kurve verändert. Diese Probleme können gelöst werden, indem man mehrere Bézierkurven miteinander verbindet. Das Ergebnis ist ein sogenannter Spline, insbesondere ein B-Spline (Basis Spline). Das Video erklärt auch, dass eine Vereinigung von quadratischen Bézierkurven einen uniformen quadratischen B-Spline und eine Vereinigung von kubischen Bézierkurven einen uniformen kubischen B-Spline bildet.

Aus den Videos können wir nützliche "Regeln" für B-Splines entnehmen:

Der erste und letzte Kontrollpunkt ist der End/Startpunkt des Splines.
Wie bei Bézierkurven beginnen Splines immer tangential zur Linie zwischen dem Startpunkt und dem ersten Kontrollpunkt (und enden tangential zur Linie zwischen dem letzten Kontrollpunkt und dem Endpunkt).
Eine Vereinigung von S Bézierkurven mit dem Grad D hat S+D Kontrollpunkte.
- Da man in den meisten Fällen mit kubischen B-Splines arbeitet, kann man sagen, dass $N$ Kontrollpunkte zu $N - 3$ Béziersegmenten und diese wiederum zu $N - 4$ Segment-Knotenpunkten führen.
Ein B-Spline mit dem Grad D bietet in jedem Punkt eine stetige Ableitung D−1 der Ordnung.
- Für einen kubischen B-Spline bedeutet dies, dass sich die Krümmung (Ableitung zweiter Ordnung) nicht ändert, wenn man von einem Segment zum nächsten reist. Dies ist eine sehr nützliche Eigenschaft, wie wir später sehen werden.

Wenn du an weiteren Details über die Eigenschaften von B-Splines interessiert bist, dann schau dir dieses Video an.

Grundlage

Da wir nur die Grundlagen von B-Splines vorstellen, gehen wir hier nicht ins Detail.

Die Basis bildet die Spline. Wenn wir uns die Definition von Bézier-Kurven im Abschnitt Mathematik ansehen, erinnern wir uns daran, dass eine Bézier-Kurve eine lineare Kombination von Polynomen ist, wobei die x/y-Koordinate jedes Kontrollpunkts als Faktor dient. Diese Polynome werden Bernstein-Polynome genannt.

Da mehrere Bézier-Kurven zu einer Spline kombiniert werden, erhalten wir eine Menge von Bernstein-Polynomen, die die Spline bilden (sie sind die Basis). Da wir die genannten Einschränkungen der Bézier-Kurven überwinden wollen, kombinieren wir die verschiedenen Bernstein-Polynome der Bézier-Kurven nicht geometrisch, sondern definieren Bernstein-Polynome über den gesamten geometrischen Bereich der Spline. Wir kombinieren also die Bézier-Kurven nicht mit ihren Bernstein-Polynomen, was wie folgt aussehen würde

Bezier - Kombination = {\begin{cases} \sum_{i = 0}^{n} P_{i} \cdot B_{i, n} (t), & 0 \leq t \leq 1 \\ \sum_{i = 0}^{n} P_{i + n} \cdot B_{i, n} (t - 1), & 1 \leq t \leq 2 \\ \dots \end{cases}

wobei $B_{i, n} (t)$ das i-te Bernstein-Polynom der Ordnung $n$ ist und die Koeffizienten $P_{i}$ die Punktkoordinaten der Kontrollpunkte der Bézier-Kurve sind. Wir verwenden jedoch einen anderen Satz von Funktionen, die über den gesamten Spline-Bereich definiert sind:

B - Spline = \sum_{i = 0}^{n} p_{i} \cdot N_{i, n} (t)

.

Man beachte, dass im Allgemeinen $N_{i, n} (t) \neq B_{i, n} (t)$ gilt und sich die Bezier-Kontrollpunkte ${P_{1}, P_{2}, \dots}$ von den B-Spline-Kontrollpunkten ${p_{1}, p_{2}, \dots}$ unterscheiden.

Die verschiedenen $N_{i, n} (t)$ sind stückweise definiert, wobei das Intervall jedes Stücks das Intervall des Bézier-Stücks ist.

Wenn die Längen aller $N_{i, n}$ Stücke gleich sind, spricht man von einer gleichmäßigen Spline. (In der Literatur wird dies oft als gleiche Laufzeit $t$ pro Stück bezeichnet.)

Um zu verstehen, wie die $p_{i}$ die Koordinaten der B-Spline-Kontrollpunkte sind, sieht man sich die erste Minute dieses Videos an: [1].

Knotenvektor

Wie oben abgeleitet, werden B-Splines aus $N_{i, n}$ stückweisen Polynomen mit Kontinuität bis zu einer bestimmten Ableitung zwischen den Stücken erstellt. Die Endpunkte des Definitionsintervalls des Stücks werden als Knoten bezeichnet. Für eine über $k$ Stücken definierte Spline gibt es $k + 1$ Knoten, die durch den sogenannten Knotenvektor gegeben sind:
${t_{0}, t_{1}, t_{2}, \dots, t_{k}}$ , wobei $t_{0} < t_{1} < t_{2} < \dots < t_{k}$

Der Knotenvektor umfasst die Knoten der $N_{i, n}$ -Basisfunktionen, die die B-Spline definieren, siehe dieses Video. Die Basisfunktionen einer B-Spline können mithilfe des Knotenvektors und eines Erstellungsalgorithmus berechnet werden, siehe dieses Video.

Die Ableitung, bis zu der Kontinuität besteht, wird durch die Multiplizität $m$ angegeben. Daher können wir für jeden Knoten einen Vektor mit der Multiplizität angeben: ${m_{0}, m_{1}, \dots, m_{k}}$ . Ein Knoten auf einer Spline mit dem Grad d und der Multiplizität m besagt, dass die Kurve links und rechts vom Knoten mindestens eine Ableitung gleicher Ordnung n hat (sogenannte Cⁿ-Stetigkeit), wobei $n = d - m$ .

Nicht-uniforme B-Splines

Die Ableitung der B-Splines von Bézier-Kurven hat die mathematische Konsequenz, dass in B-Splines jeder Polynomabschnitt dieselbe Länge hat. Solche B-Splines werden uniform genannt. Der allgemeinere Fall ist, dass sie dieselbe Längen haben können aber nicht müssen. Diese nicht-uniformen Splines haben den Vorteil, man kontrollieren kann, wie dicht die Splines an den Kontrollpunkten vorbeilaufen.

Mathematisch wird dies erreicht, indem die verschiedenen $N_{i, n}$ -Stücke in unterschiedlichen Intervallen definiert werden. Wenn beispielsweise eine B-Spline für das Intervall [0, 1] definiert ist, ist sie gleichmäßig, wenn alle ihre beispielsweise 5 Teile ebenfalls in diesem Intervall definiert sind. Wenn nun $N_{1, 4}$ nur im Intervall [0, 0,6] definiert ist (außerhalb des Intervalls ist es auf Null gesetzt), ist es kürzer und somit wird die Spline ungleichmäßig.

Wie oben beschrieben, werden die Parameter der Knoten durch den Knotenvektor beschrieben. Der Knotenvektor speichert also die Definitionsintervalle. Wenn nun ein Teil ein anderes Intervall erhält, ändert sich auch der Knotenvektor. Eine Visualisierung findet man in diesem Video.

Rationale B-splines

Eine weitere Verallgemeinerung lässt sich für B-Splines durch die Einführung von Gewichten für die Kontrollpunkte vornehmen. Auf diese Weise lässt sich steuern, "wie wichtig" ein Kontrollpunkt ist.

Die Gleichung für eine solche Spline lautet

c (n, t) = \frac{\sum_{i = 0}^{n} d_{i} N_{i, n} (t) \cdot w_{i}}{\sum_{i = 0}^{n} N_{i, n} (t) \cdot w_{i}}

Man beachte, dass die Funktion nun kein Polynom mehr ist, sondern eine rationale Funktion, und diese Splines werden als rationale B-Splines bezeichnet. Man beachte, dass sich die Gleichung zu einer regulären nicht-rationalen B-Spline vereinfacht, wenn alle $w_{i}$ gleich sind. Nicht-rationale B-Splines sind also eine Untergruppe der rationalen B-Splines.

Nicht-uniforme und rationale B-Splines werden oft NURBS genannt und werden in vielen Bereichen des geometrischen Modellierens eingesetzt.

B-splines in FreeCAD

FreeCAD bietet die Möglichkeit, uniforme oder nicht-uniforme B-Splines beliebigen Grades in 2D über die Skizzierer Arbeitsbereich zu erstellen.

Erstellung

Um B-Splines zu erstellen, gehe in eine Skizze und verwende die Werkzeugleistenschaltfläche B-spline erstellen. Dann Linksklick um einen Kontrollpunkt zu setzen, bewege die Maus Linksklick, um den nächsten Kontrollpunkt zu setzen und so weiter. Abschließend Rechtsklick, um die Definition abzuschließen und den B-Spline zu erstellen.

Standardmäßig werden uniforme kubische Splines erstellt, es sei denn, es stehen nicht genügend Kontrollpunkte zur Verfügung, um dies zu tun. Wird also einen B-Spline mit nur 2 Kontrollpunkten erstellt, erhält man natürlich einen Spline, der eine einzelne lineare Bézierkurve ist, mit 3 Kontrollpunkte erhält man eine quadratische Bézierkurve, erst mit 5 Kontrollpunkten erhält man einen kubischen B-Spline, der aus 2 Béziersegmenten besteht. eingeführt in 0.20 Wird während der Erstellung eines B-Splines D gedrückt, kann sein Grad festgelegt werden (er wird auf einen geringeren Grad gesetzt, wenn nicht genügend punkte vorhanden sind).

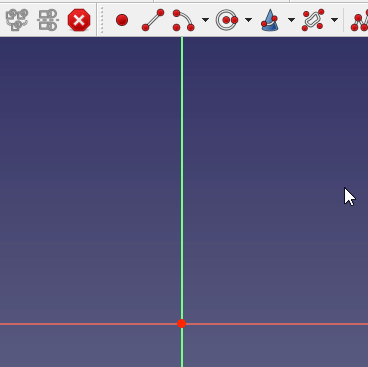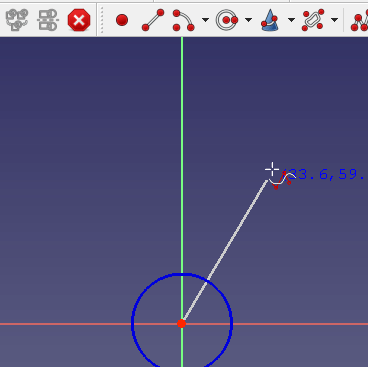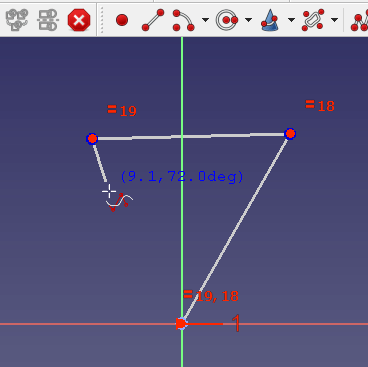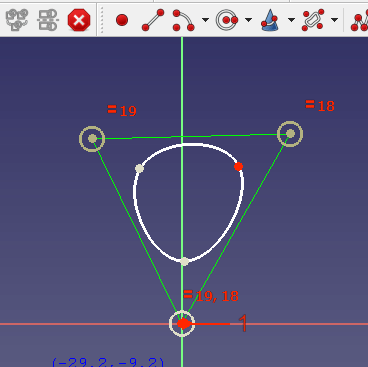
Um periodische B-Splines (B-Splines, die eine geschlossene Kurve bilden) zu erstellen, verwende die Werkzeugleistenschaltfläche Periodische B-spline. Es ist nicht notwendig, den letzten Kontrollpunkt auf den ersten zu setzen, da der B-Spline automatisch geschlossen wird:

B-Splines können auch aus bestehenden Skizzen-Segmenten erzeugt werden. Dazu die Elemente auswählen und drücke die Schaltfläche Geometrie in B-Spline wandeln drücken.

Während der Erstellung eines B-Splines kann sein Grad angegeben werden, indem die Taste D gedrückt wird. Hiermit kann die Voreinstellung, die Erstellung eines kubischen B-Splines, überschrieben werden. eingeführt in 0.20

Ändern des Grads

Um den Grad zu ändern, wähle den B-Spline und verwende entweder die Werkzeugleistenschaltfläche B-Spline-Grad erhöhen oder B-Spline-Grad vermindern.

Hinweis: Das Verringern des Grads kann eine vorherige Erhöhung des Grads nicht rückgängig machen, siehe die Wiki Seite B-spline Grad vermindern für eine Erklärung.

Ändern der Knotenvielfalt

Die Punkte, an denen zwei Bézierkurven miteinander verbunden werden, um den B-Spline zu bilden, werden Knoten genannt. Die Knotenmultiplikation bestimmt, wie die Bézier Teile verbunden werden, siehe die Wiki Seite Knotenvielfalt erhöhen für Details.

Um die Knotenvielfalt zu ändern, verwende die Werkzeugleistenschaltflächen in der B-spline Knotenvielfalt erhöhen oder B-spline Knotenvielfalt vermindern.

Hinweis: Das Erstellen von zwei B-Splines, die miteinander verbunden sind, wird sich nicht zu einem einzigen neuen B-Spline vereinigen. Ihr Verbindungspunkt ist also kein Knoten. Die einzige Möglichkeit, einen neuen Knoten in einem bestehenden B-Spline zu erhalten, besteht darin, den Grad zu verringern. Dabei können jedoch viele neue Knoten entstehen. Daher ist es besser, den B-Spline mit mehr Kontrollpunkten neu zu zeichnen.

Ändern des Gewichts

Um jeden Kontrollpunkt herum siehst du einen dunkelgelben Kreis. Sein Radius legt das Gewicht für den entsprechenden Kontrollpunkt fest. Standardmäßig haben alle Kreise den Radius 1. Dies wird durch eine Radiusbeschränkung für den ersten Kontrollpunktkreis angezeigt.

Um eine rationale B-Spline zu erstellen, müssen die Gewichte unabhängig voneinander sein. Dazu können Sie die Einschränkung, dass alle Kreise gleich sind, löschen und dann unterschiedliche Radiusbeschränkungen für die Kreise festlegen.

Wenn keine Radiusbeschränkung festgelegt ist, kannst du den Radius auch durch Ziehen ändern:

Am Beispiel des Ziehens siehst du, dass ein hohes Gewicht die Kurve zum Kontrollpunkt zieht, während ein sehr niedriges Gewicht die Kurve so verändert, als ob der Kontrollpunkt fast nicht existiert.

Betrachtet man die Funktion zur Erstellung nicht-uniformer rationaler B-Splines, erkennt man, dass ein Gewicht von Null zu einer Division durch Null führen würde. Negative Gewichte sind theoretisch möglich, werden aber nicht unterstützt. Daher können nur Gewichte größer als Null angegenben werden.

Hinweis: Beim Ziehen von Punkten, Knoten oder Breiten ändern sich die Kreisdurchmesser, die das Gewicht anzeigen. Dies liegt daran, dass der Durchmesser aus Gründen der Visualisierung von der Gesamtlänge der B-Spline abhängt. Das tatsächliche Gewicht wird nicht verändert.

Knoten barbeiten

Neue Knoten (Kontrollpunkte) können mit der Schaltfläche Knoten einfügen hinzugefügt werden. eingeführt in 0.20

Ein Knoten wird gelöscht, wenn sein Grad auf 0 verkleinert wird (d.h. dass Vielfachheit eines Spline-Knotens verringern angewendet wird, wenn sein Grad 1 beträgt).

Das Ändern des Parameterwerts eines Knotens wird noch nicht unterstützt.

Informationen anzeigen

Da die Form eines B-Splines nicht viel über seine Eigenschaften aussagt, bietet FreeCAD verschiedene Werkzeuge, um die Eigenschaften anzuzeigen:

Eigenschaft	Schaltfläche in der Werkzeugleiste
Grad	B-Spline-Grad ein- / ausblenden
Kontrollpolygon	B-Spline-Kontrollpolygon ein- / ausblenden
Krümmungskamm	B-Spline-Krümmungskamm ein- / ausblenden
Knotenvielfachheit	Vielfachheit der B-Spline-Knoten ein- / ausblendenn
Knotengewichte	Gewicht der B-Spline-Kontrollpunkte anzeigen / ausblenden

Einschränkungen

Aktuell (FreeCAD 0.20) gibt es einige Einschränkungen bei der Verwendung von Splines, die man kennen sollte:

Es können keine tangentialen Randbedingungen festgelegt werden.
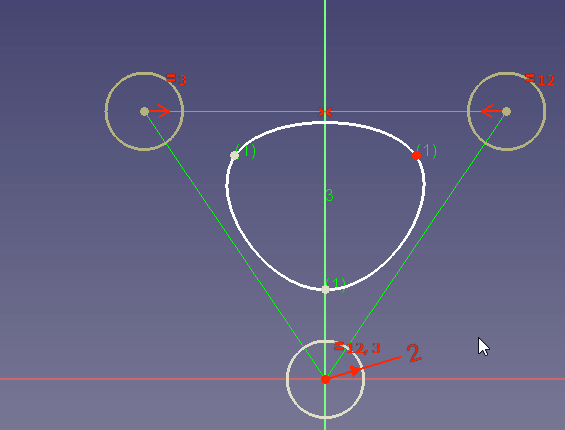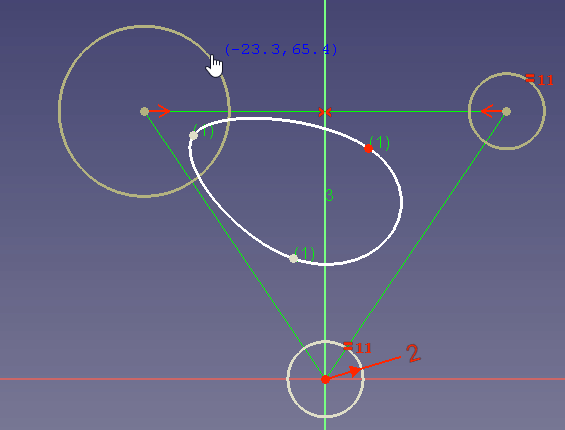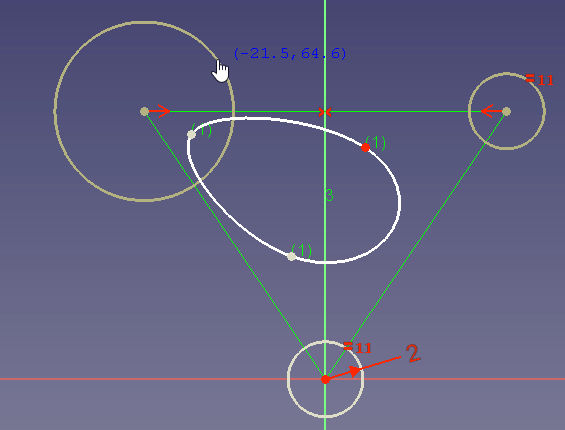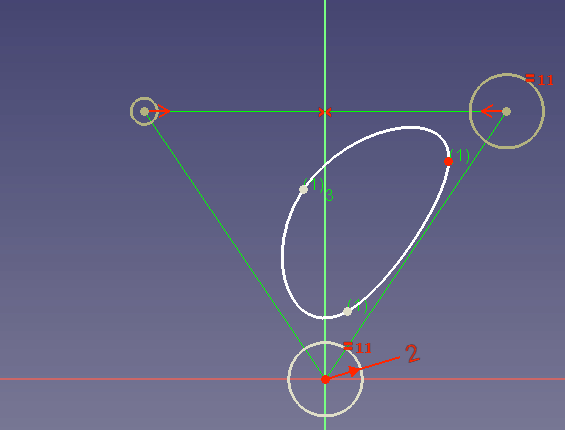
In diesem Beispiel

soll sichergestellt werden, dass der Spline die blaue Kurve 2 mal tangential berührt. Dies ist sinnvoll, wenn die blaue Linie z.B. die räumliche Grenze eines Entwurfs darstellt.
Es kann keine Versatzkurve für einen B-Spline mit dem Werkzeug Draft Versatz erstellt werden.

Typische Anwendungsfälle

Entsprechend den Eigenschaften von B-Splines gibt es 3 Hauptanwendungsfälle:

Kurven, die tangential zu einer bestimmten Richtung beginnen/enden. Ein Beispiel hierfür ist das Motivationsbeispiel oben.
Kurven, die größere Entwürfe beschreiben und die Freiheit lokaler Änderungen bieten. Siehe dieses Beispiel unten.
Kurven, die eine gewisse Stetigkeit (Ableitung) bieten. Siehe dieses Beispiel unten.

Gestaltung

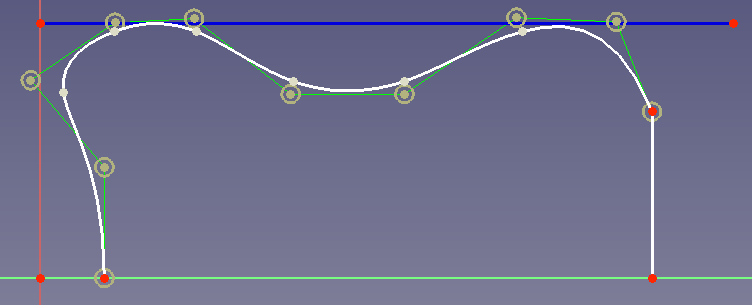
Nimm zum Beispiel den Fall, dass du ein Gehäuse für eine Küchenmaschine entwirfst. Die gewünschte Form sollte wie diese aussehen:

Für die Definition der äußeren Form ist es vorteilhaft, einen B-Spline zu verwenden, denn wenn du einen Kontrollpunkt änderst, um die Krümmung an der Unterseite zu ändern, wird die Krümmung an den Seiten und oben nicht geändert:

Stetigkeit an geometrischen Übergängen

Es gibt mehrere Fälle, in denen es physikalisch notwendig ist, an geometrischen Übergängen eine gewisse Oberflächenkontinuität zu haben. Nimm zum Beispiel die Innenwände eines Flüssigkeitskanals. Wenn sich der Durchmesser des Kanals ändert, möchte man keine Kante haben, da Kanten zu Turbulenzen führen würden. Daher verwendet man, wie im Motivationsbeispiel oben, Splines für diesen Zweck.

Auslöser für die Entwicklung der Bézierkurven war zunächst die französische Autoindustrie. Neben der Einsparung von Material und der Verringerung des Luftwiderstands sollte auch das Aussehen der Autos verbessert werden. Und wenn man sich das schicke Design französischer Autos aus den 60er und 70er Jahren anschaut, sieht man, dass die Bézierkurven dem Autodesign einen Schub gegeben haben.

Nehmen wir zum Beispiel diese Aufgabe bei der Gestaltung von Autos: Der Autokotflügel soll "schön" aussehen. Hier ist eine grundlegende Skizze unserer Aufgabe:

"Schön aussehen" bedeutet, dass der (potenzielle) Kunde den Kotflügel betrachtet und keine unerwarteten Lichtreflexe und auch keine plötzlichen Veränderungen in der Reflexion des Autolacks sieht. Was brauchst du also, um Veränderungen in den Reflexionen zu vermeiden? Genaues Hinsehen auf den Kotflügel:

Im räumlichen Bereich oberhalb der Kante ist die Intensität des reflektierten Lichts gering (gekennzeichnet durch die rote Ellipse), da kein Licht direkt in die Richtung von der Kante zum Auge reflektiert wird.

Du siehst, wenn es eine Kante gibt, gibt es einen räumlichen Bereich, in dem das reflektierte Licht eine geringere Intensität hat, und das ist es, was du beim Betrachten des Kotflügels bemerken wirst. Um dies zu vermeiden, brauchst du eine kontinuierliche Änderung der Neigung deiner Oberflächenelemente. Die Steigung ist die Ableitung erster Ordnung und wie im Abschnitt Grundlagen erklärt, bietet ein B-Spline zweiten Grades (quadratisch) an jedem Punkt eine kontinuierliche Ableitung erster Ordnung.

Aber ist das wirklich ausreichend? Am Punkt des geometrischen Übergangs haben wir nun auf beiden Seiten die gleiche Steigung, aber die Steigung kann sich auf beiden Seiten unterschiedlich verändern. Dann haben wir diese Situation:

Wir haben also auch räumliche Bereiche, in denen die Intensität des reflektierten Lichts unterschiedlich ist. Um dies zu vermeiden, benötigen wir am geometrischen Übergangspunkt auch eine Stetigkeit der Ableitung zweiter Ordnung und damit einen kubischen B-Spline.