Topological data scripting/ru

Other languages:

Программируемые объекты

Оглавление

Введение

Здесь мы объясним вам, как управлять верстаком Part непосредственно из интерпретатора Python FreeCAD или из любого внешнего сценария. Основы создания сценариев топологических данных описаны в объяснение концепции модуля Part. Обязательно просмотрите раздел Scripting и страницы Основы скриптинга FreeCAD, если вам нужна дополнительная информация о том, как работает python-скриптинг во FreeCAD .

Смотрите также

Диаграмма классов

Это обзор наиболее важных классов модуля Part через Unified Modeling Language (UML):

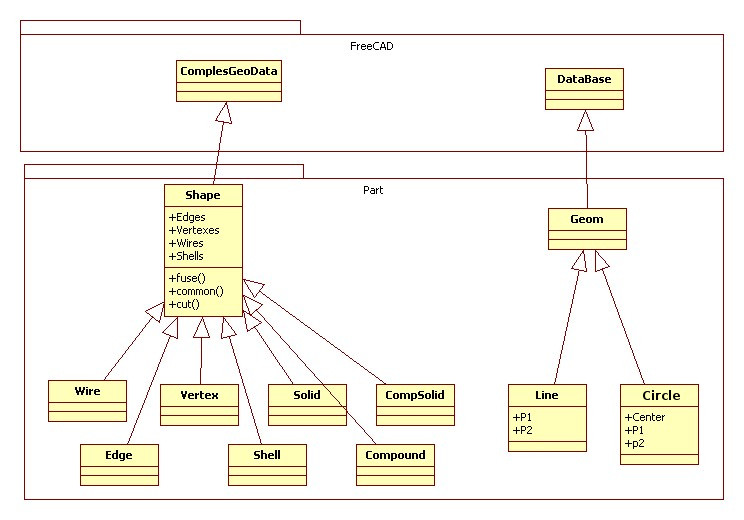
Классы Python, содержащиеся в модуле Part

Геометрия

Геометрические объекты являются строительными блоками для всех топологических объектов:

Geom Базовый класс геометрических объектов.
Line Прямая линия в 3D, задается начальной и конечной точкой.
Circle Окружность или дуга задается центром, начальной и конечной точкой.
и так далее...

Топология

Доступны нижеследующие топологические типы данных:

COMPOUND Группа из топологических объектов любого типа.
COMPSOLID Составное твердое тело, как набор твердых тел соединенными гранями. Он расширяет понятие Ломаной кривой(WIRE) и оболочки(SHELL) для твердых тел.
SOLID Часть пространства ограниченная оболочкой. Она трехмерная.
SHELL Набор граней соединенных между собой через ребра. Оболочки могут быть открытыми или закрытыми.
FACE В 2D это часть плоскости; в 3D это часть поверхности. Это геометрия ограничена (обрезана) по контурам. Она двухмерная.
WIRE Набор ребер соединенных через вершины. Он может быть как открытым, так и закрытым в зависимости от того связаны ли крайние ребра или нет.
EDGE Топологический элемент соответствующий ограниченной кривой. Ребро как правило ограничивается вершинами. Оно одномерное.
VERTEX Топологический элемент соответствующий точке. Обладает нулевой размерность.
SHAPE общий термин охватывающий все выше сказанное.

Примеры: Создание простейшей топологии

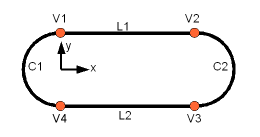
Теперь мы создадим топологию из геометрических примитивов. Для изучения мы используем деталь(part), как показано на картинке состоящую из четырех вершин, двух окружностей и двух линий.

Создание геометрии

В начале мы должны создать отдельную деталь из данной ломаной. И мы должны убедиться что вершины геометрических частей расположены на тех же позициях. В противном случае позже мы не смогли бы соединить геометрические части в топологию!

Итак, сначала мы создаем точки:

import FreeCAD as App
import Part
V1 = App.Vector(0, 10, 0)
V2 = App.Vector(30, 10, 0)
V3 = App.Vector(30, -10, 0)
V4 = App.Vector(0, -10, 0)

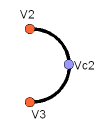
Дуга

Для каждой дуги нам нужно создать вспомогательную точку и провести дугу через три точки:

VC1 = App.Vector(-10, 0, 0)
C1 = Part.Arc(V1, VC1, V4)
VC2 = App.Vector(40, 0, 0)
C2 = Part.Arc(V2, VC2, V3)

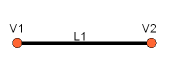
Линия

Сегменты линии могут быть созданы из двух точек:

L1 = Part.LineSegment(V1, V2)
L2 = Part.LineSegment(V3, V4)

Соединяем все вместе

Последний шаг - собираем все основные геометрические элементы вместе и получаем форму:

S1 = Part.Shape([C1, L1, C2, L2])

Создание призмы

Теперь вытягиваем ломанную по направлению и фактически получаем 3D форму:

W = Part.Wire(S1.Edges)
P = W.extrude(App.Vector(0, 0, 10))

Показать всё

Part.show(P)

Создание простых фигур

Вы легко можете создавать простые топологические объекты с помощью методов make...() содержащихся в модуле Part:

b = Part.makeBox(100, 100, 100)
Part.show(b)

Доступные make...() методы:

makeBox(l,w,h,[p,d]) : создает прямоугольник, с началом в точке p и вытянутый в направлении d с размерами (l,w,h) По умолчанию p установлен как Vector(0,0,0) и d установлен как Vector(0,0,1)
makeCircle(radius,[p,d,angle1,angle2]) -- Создает окружность с заданным радиусом. По умолчанию p=Vector(0,0,0), d=Vector(0,0,1), angle1=0 и angle2=360
makeCone(radius1,radius2,height,[p,d,angle]) -- Создает конус с заданным радиусами и высотой. По умолчанию p=Vector(0,0,0), d=Vector(0,0,1) и angle=360
makeCylinder(radius,height,[p,d,angle]) -- Создает цилиндр с заданным радиусом и высотой. По умолчанию p=Vector(0,0,0), d=Vector(0,0,1) и angle=360
makeLine((x1,y1,z1),(x2,y2,z2)) -- Создает линию проходящую через две точки
makePlane(length,width,[p,d]) -- Создает плоскость с заданной длинной и шириной. По умолчанию p=Vector(0,0,0) и d=Vector(0,0,1)
makePolygon(list) -- Создает многоугольник из списка точек
makeSphere(radius,[p,d,angle1,angle2,angle3]) -- Создает сферу с заданным радиусом. По умолчанию p=Vector(0,0,0), d=Vector(0,0,1), angle1=0, angle2=90 и angle3=360
makeTorus(radius1,radius2,[p,d,angle1,angle2,angle3]) -- Создает тор по заданными радиусам.По умолчанию p=Vector(0,0,0), d=Vector(0,0,1), angle1=0, angle2=360 и angle3=360

На странице Part API приведен полный список доступных методов модуля Part.

Импорт необходимых модулей

В начале нам нужно импортировать модуль Part, чтобы мы могли использовать его содержимое в Python. Также импортируем модуль Base из модуля FreeCAD:

import FreeCAD as App
import Part

Создание вектора

Векторы являются одними из самых важных частей информации при построении фигур. Они обычно содержат три числа (но не всегда): декартовы координаты x, y и z. Для создания вектора введите:

myVector = App.Vector(3, 2, 0)

Мы только что создали вектор с координатами x = 3, y = 2, z = 0. В модуле Part векторы используются повсеместно. Формы детали также используют другой тип представления точек, называемый Vertex, который является просто контейнером для вектора. Вы можете получить доступ к вектору вершины следующим образом:

myVertex = myShape.Vertexes[0]
print(myVertex.Point)
> Vector (3, 2, 0)

Создание ребра

Ребра это не что иное, как линия с двумя вершинами:

edge = Part.makeLine((0, 0, 0), (10, 0, 0))
edge.Vertexes
> [<Vertex object at 01877430>, <Vertex object at 014888E0>]

Примечание: Вы можете создать ребро передав два вектора.

vec1 = App.Vector(0, 0, 0)
vec2 = App.Vector(10, 0, 0)
line = Part.LineSegment(vec1, vec2)
edge = line.toShape()

Вы можете узнать длину и центр ребра, вот так:

edge.Length
> 10.0
edge.CenterOfMass
> Vector (5, 0, 0)

Вывод фигуры на экран

До сих пор мы создали объект ребро, но не увидели его на экране. Это связано с тем, что 3D-сцена FreeCAD отображает только то, что указано для отображения. Для этого мы используем этот простой метод:

Part.show(edge)

Функция show создает объект "shape" в нашем FreeCAD документе. Используйте это всякий раз, когда пришло время показать свое творение на экране.

Создание ломанной кривой

Ломаная представляет собой многогранную линию и может быть создан из списка ребер или даже из списка ломаных:

edge1 = Part.makeLine((0, 0, 0), (10, 0, 0))
edge2 = Part.makeLine((10, 0, 0), (10, 10, 0))
wire1 = Part.Wire([edge1, edge2]) 
edge3 = Part.makeLine((10, 10, 0), (0, 10, 0))
edge4 = Part.makeLine((0, 10, 0), (0, 0, 0))
wire2 = Part.Wire([edge3, edge4])
wire3 = Part.Wire([wire1, wire2])
wire3.Edges
> [<Edge object at 016695F8>, <Edge object at 0197AED8>, <Edge object at 01828B20>, <Edge object at 0190A788>]
Part.show(wire3)

Part.show(wire3) пакажет 4 ребра, из которых состоит наша ломаная линяи. Другая полезная информация может быть легко найдена:

wire3.Length
> 40.0
wire3.CenterOfMass
> Vector (5, 5, 0)
wire3.isClosed()
> True
wire2.isClosed()
> False

Создание грани

Только грани, созданные из замкнутых ломаных, будут действительными. В этом примере wire3 является замкнутой ломаной, но wire2 не является замкнутым (см. выше)

face = Part.Face(wire3)
face.Area
> 99.99999999999999
face.CenterOfMass
> Vector (5, 5, 0)
face.Length
> 40.0
face.isValid()
> True
sface = Part.Face(wire2)
sface.isValid()
> False

Только грани имеют поверхность, а ломанные и ребра нет.

Создание окружности

Окружность может быть создана, например так:

circle = Part.makeCircle(10)
circle.Curve
> Circle (Radius : 10, Position : (0, 0, 0), Direction : (0, 0, 1))

Если вы хотите создать её с определенным положением и в определенном направлении

ccircle = Part.makeCircle(10, App.Vector(10, 0, 0), App.Vector(1, 0, 0))
ccircle.Curve
> Circle (Radius : 10, Position : (10, 0, 0), Direction : (1, 0, 0))

ccircle будет создана на расстоянии 10 от начала координат x и будет направлена вдоль оси x. Примечание: makeCircle принимает только тип Base.Vector() в качестве позиции и нормали. Вы также можете создать часть окружности, задав начальный и конечный угол:

from math import pi
arc1 = Part.makeCircle(10, App.Vector(0, 0, 0), App.Vector(0, 0, 1), 0, 180)
arc2 = Part.makeCircle(10, App.Vector(0, 0, 0), App.Vector(0, 0, 1), 180, 360)

Обе arc1 и arc2 вместе составляют окружность. Углы задаются в градусах, если вы хотите задать радианами, просто преобразуйте используя формулу: degrees = radians * 180/PI или используя math модуль python-а (прежде, конечно, выполнив import math): degrees = math.degrees(radians)

import math
degrees = math.degrees(radians)

Создать дугу по точкам

К сожалению нет функции makeArc, но у нас есть функция Part.Arc для создания дуги через три точки. Она создает объект дуги, соединяющий начальную точку с конечной точкой через среднюю точку. Функция .toShape() объекта дуги должна вызываться для получения объекта ребра, так же, как при использовании Part.LineSegment вместо Part.makeLine.

arc = Part.Arc(App.Vector(0, 0, 0), App.Vector(0, 5, 0), App.Vector(5, 5, 0))
arc
> <Arc object>
arc_edge = arc.toShape()
Part.show(arc_edge)

Arc принимает только Base.Vector() для точек. arc_edge - это то, что нам нужно, и мы можем отобразить его с помощью Part.show(arc_edge). Вы также можете получить дугу, используя часть круга:

from math import pi
circle = Part.Circle(App.Vector(0, 0, 0), App.Vector(0, 0, 1), 10)
arc = Part.Arc(circle,0,pi)

Дуги являются действительными ребрами, такими как линии, поэтому их можно использовать и в ломаных линиях.

Создать многоугольник (полигон)

Линия по нескольким точкам, не что иное как создание ломаной с множеством ребер. функция makePolygon берет список точек и создает ломанную по этим точкам:

lshape_wire = Part.makePolygon([App.Vector(0, 5, 0), App.Vector(0, 0, 0), App.Vector(5, 0, 0)])

Создание кривой Безье

Кривые Безье используются для моделирования гладких кривых с использованием ряда полюсов (точек) и необязательных весов. Функция ниже делает Part.BezierCurve из ряда точек FreeCAD.Vector. (Примечание: при «получении» и «установке» одного полюса или веса индексы начинаются с 1, а не с 0.)

def makeBCurveEdge(Points):
   geomCurve = Part.BezierCurve()
   geomCurve.setPoles(Points)
   edge = Part.Edge(geomCurve)
   return(edge)

Создание плоскости

Плоскость это ровная поверхность, в смысле 2D грань. Метод создания её это makePlane(length,width,[start_pnt,dir_normal]). По умолчанию start_pnt=Vector(0,0,0) и dir_normal=Vector(0,0,1). Используя dir_normal = Vector(0,0,1) создаёт плоскость, обращённую к положительному направлению оси z, в то время как dir_normal=Vector(1,0,0) создаёт плоскость обращённую к положительному направлению оси х:

plane = Part.makePlane(2, 2)
plane
> <Face object at 028AF990>
plane = Part.makePlane(2, 2, App.Vector(3, 0, 0), App.Vector(0, 1, 0))
plane.BoundBox
> BoundBox (3, 0, 0, 5, 0, 2)

BoundBox является параллелепипед вмещающих плоскость с диагональю, начиная с (3,0,0) и концом в (5,0,2). Здесь толщина BoundBoxпо оси y равна нулю, поскольку его форма полностью плоская.

Примечание: makePlane доступны только Base.Vector() для задания start_pnt и dir_normal а не кортежи

Создание эллипса

Эллипс можно создать несколькими способами:

Part.Ellipse()

Создает эллипс с большой полуосью 2 и малой полуосью 1 с центром в (0,0,0)

Part.Ellipse(Ellipse)

Создает копию данного эллипса.

Part.Ellipse(S1, S2, Center)

Создаст эллипс с центров точке Center, где плоскость эллипса определяет Center, S1 и S2, это большая ось ззаданная Center и S1, это больший радиус расстояние между Center и S1, и меньший радиус это расстояние между S2 и юольшей осью.

Part.Ellipse(Center, MajorRadius, MinorRadius)

Создает эллипс с большим и меньшим радиусом MajorRadius и MinorRadius, расположенными в плоскости заданной точкой Center и нормалью (0,0,1)

eli = Part.Ellipse(App.Vector(10, 0, 0), App.Vector(0, 5, 0), App.Vector(0, 0, 0))
Part.show(eli.toShape())

В приведенном выше коде мы ввели S1, S2 и center. Аналогично Дуге, Эллипс также создает объект, а не ребро, так что мы должны превратить его в ребро используя toShape() для отображения

Примечание: Дуга допускает только Base.Vector() для задания точек, а не кортеж.

eli = Part.Ellipse(App.Vector(0, 0, 0), 10, 5)
Part.show(eli.toShape())

для вышеуказанного конструктора Ellipse мы передали center, MajorRadius и MinorRadius.

Создание тора

Используя makeTorus(radius1,radius2,[pnt,dir,angle1,angle2,angle]). По умолчанию pnt=Vector(0,0,0), dir=Vector(0,0,1), angle1=0,angle2=360 и angle=360

Рассмотрим тор как маленький круг, вытянутый вдоль большого круга. Radius1 это радиус большого круга, radius2 это радиус малого круга, pnt это центр тора и dir это направление нормали. angle1 и angle2 углы в радианах для малого круга, последний параметр angle для создания секцию (части) тора:

torus = Part.makeTorus(10, 2)

В коде выше, был создан тор с диаметром 20 (радиус 10) и толщиной 4 (малая окружность радиусом 2)

tor=Part.makeTorus(10, 5, App.Vector(0, 0, 0), App.Vector(0, 0, 1), 0, 180)

В приведенном выше коде, создан кусочек тора.

tor=Part.makeTorus(10, 5, App.Vector(0, 0, 0), App.Vector(0, 0, 1), 0, 360, 180)

В приведенном выше коде, создан полу-тор, изменен только последний параметр. Т.е. angle а остальные углы установлены по умолчанию. Подстановка угла 180 создаст тор от 0 до 180, т.е. половину тора.

Создание параллелепипеда или кубоида

Используя makeBox(length,width,height,[pnt,dir]), создаем блок расположенный в pnt с размерами (length,width,height). По умолчанию pnt=Vector(0,0,0) и dir=Vector(0,0,1).

box = Part.makeBox(10, 10, 10)
len(box.Vertexes)
> 8

Создание сферы

Используя makeSphere(radius,[pnt, dir, angle1,angle2,angle3]). По умолчанию pnt=Vector(0,0,0), dir=Vector(0,0,1), angle1=-90, angle2=90 и angle3=360. angle1 и angle2 это вертикальный минимум и максимум сферы (срезает часть сферы снизу или сверху), angle3 is the sphere diameter (определяет замкнутое ли это тело вращения или его секция).

sphere = Part.makeSphere(10)
hemisphere = Part.makeSphere(10, App.Vector(0, 0, 0), App.Vector(0, 0, 1), -90, 90, 180)

Создание цилиндра

Используя makeCylinder(radius,height,[pnt,dir,angle]), создается цилиндр с указанным радиусом и высотой. По умолчанию pnt=Vector(0,0,0),dir=Vector(0,0,1) и angle=360.

cylinder = Part.makeCylinder(5, 20)
partCylinder = Part.makeCylinder(5, 20, App.Vector(20, 0, 0), App.Vector(0, 0, 1), 180)

Cоздание конуса

Используя makeCone(radius1,radius2,height,[pnt,dir,angle]), создаем конус с указанными радиусами и высотой. По умолчанию pnt=Vector(0,0,0), dir=Vector(0,0,1) и angle=360.

cone = Part.makeCone(10, 0, 20)
semicone = Part.makeCone(10, 0, 20, App.Vector(20, 0, 0), App.Vector(0, 0, 1), 180)

Modify shapes

There are several ways to modify shapes. Some are simple transformation operations such as moving or rotating shapes, others are more complex, such as unioning and subtracting one shape from another.

Transform operations

Translate a shape

Translating is the act of moving a shape from one place to another. Any shape (edge, face, cube, etc...) can be translated the same way:

myShape = Part.makeBox(2, 2, 2)
myShape.translate(App.Vector(2, 0, 0))

This will move our shape "myShape" 2 units in the X direction.

Rotate a shape

To rotate a shape, you need to specify the rotation center, the axis, and the rotation angle:

myShape.rotate(App.Vector(0, 0, 0),App.Vector(0, 0, 1), 180)

The above code will rotate the shape 180 degrees around the Z Axis.

Matrix transformations

A matrix is a very convenient way to store transformations in the 3D world. In a single matrix, you can set translation, rotation and scaling values to be applied to an object. For example:

myMat = App.Matrix()
myMat.move(App.Vector(2, 0, 0))
myMat.rotateZ(math.pi/2)

Note: FreeCAD matrixes work in radians. Also, almost all matrix operations that take a vector can also take three numbers, so these two lines do the same thing:

myMat.move(2, 0, 0)
myMat.move(App.Vector(2, 0, 0))

Once our matrix is set, we can apply it to our shape. FreeCAD provides two methods for doing that: transformShape() and transformGeometry(). The difference is that with the first one, you are sure that no deformations will occur (see Scaling a shape below). We can apply our transformation like this:

myShape.transformShape(myMat)

или

myShape.transformGeometry(myMat)

Scale a shape

Scaling a shape is a more dangerous operation because, unlike translation or rotation, scaling non-uniformly (with different values for X, Y and Z) can modify the structure of the shape. For example, scaling a circle with a higher value horizontally than vertically will transform it into an ellipse, which behaves mathematically very differently. For scaling, we cannot use the transformShape(), we must use transformGeometry():

myMat = App.Matrix()
myMat.scale(2, 1, 1)
myShape=myShape.transformGeometry(myMat)

Булевы Операции

Как вырезать одну форму из других?

cut(...) - Вычисление различий задано в топологическом классе shape.

Subtracting a shape from another one is called "cut" in FreeCAD and is done like this:

cylinder = Part.makeCylinder(3, 10, App.Vector(0, 0, 0), App.Vector(1, 0, 0))
sphere = Part.makeSphere(5, App.Vector(5, 0, 0))
diff = cylinder.cut(sphere)

Как получить пересечение двух форм?

Тем же способом, пересечение между двумя фигурами называется "common(...)" (пересечение задано в топологическом классе shape) и делается так:

The same way, the intersection between two shapes is called "common" and is done this way:

cylinder1 = Part.makeCylinder(3, 10, App.Vector(0, 0, 0), App.Vector(1, 0, 0))
cylinder2 = Part.makeCylinder(3, 10, App.Vector(5, 0, -5), App.Vector(0, 0, 1))
common = cylinder1.common(cylinder2)

Как объединить две формы?

fuse(...) - Объединение задано в топологическом классе shape

Union is called "fuse" and works the same way:

cylinder1 = Part.makeCylinder(3, 10, App.Vector(0, 0, 0), App.Vector(1, 0, 0))
cylinder2 = Part.makeCylinder(3, 10, App.Vector(5, 0, -5), App.Vector(0, 0, 1))
fuse = cylinder1.fuse(cylinder2)

Как получить сечение тела и заданной формы?

Section это пересечение твердого тела и плоской фигуры (сечение задано в топологическом классе shape). Вернет секущую кривую, составную кривую, состоящую из ребер.

A "section" is the intersection between a solid shape and a plane shape. It will return an intersection curve, a compound curve composed of edges.

cylinder1 = Part.makeCylinder(3, 10, App.Vector(0, 0, 0), App.Vector(1, 0, 0))
cylinder2 = Part.makeCylinder(3, 10, App.Vector(5, 0, -5), App.Vector(0, 0, 1))
section = cylinder1.section(cylinder2)
section.Wires
> []
section.Edges
> [<Edge object at 0D87CFE8>, <Edge object at 019564F8>, <Edge object at 0D998458>, 
 <Edge  object at 0D86DE18>, <Edge object at 0D9B8E80>, <Edge object at 012A3640>, 
 <Edge object at 0D8F4BB0>]

Выдавливание

Выдавливание - это процесс «выпячивания» плоской фигуры в определенном направлении, становящейся твердым телом. Представьте, как «выпячивание» круга сделало его трубой:

Extrusion is the act of "pushing" a flat shape in a certain direction, resulting in a solid body. Think of a circle becoming a tube by "pushing it out":

circle = Part.makeCircle(10)
tube = circle.extrude(App.Vector(0, 0, 2))

Если ваш круг полый, вы получите полую трубу. Если ваш круг это диск с заполненной поверхностью, вы получите сплошной цилиндр:

wire = Part.Wire(circle)
disc = Part.Face(wire)
cylinder = disc.extrude(App.Vector(0, 0, 2))

Исследование Форм

Вы легко можете исследовать структуру топологических данных:

You can easily explore the topological data structure:

import Part
b = Part.makeBox(100, 100, 100)
b.Wires
w = b.Wires[0]
w
w.Wires
w.Vertexes
Part.show(w)
w.Edges
e = w.Edges[0]
e.Vertexes
v = e.Vertexes[0]
v.Point

Если ввести строчку выше в интерпретатор python , вы получите хорошее представление об устройстве объектов Part. Здесь наша команда makeBox() создает твердое тело. Это тело, как и все тела Part, содержит грани. Грани всегда содержат ломанные, которые являются набором ребер ограничивающих грань. Каждая грань обладает минимум одной замкнутой ломаной (может больше, если есть отверстие). В ломанной мы можем посмотреть на каждое ребро отдельно, и по краям каждого ребра мы можем увидеть вершины. Прямые ребра обладают только двумя вершинами, разумеется. Вершины модуля Part являются формами OCC(OpenCascade), но они обладают атрибутом Point, который возвращает вектор FreeCAD.

Исследование Рёбер

В случае ребра, которое является произвольной кривой, вы наверняка захотите произвести дискретизицию. В FreeCAD ребра задаются с помощью параметра длинны. Это означает что вы можете перемещатся вдоль ребра/кривой задавая длинну:

In case of an edge, which is an arbitrary curve, it's most likely you want to do a discretization. In FreeCAD the edges are parametrized by their lengths. That means you can walk an edge/curve by its length:

import Part
box = Part.makeBox(100, 100, 100)
anEdge = box.Edges[0]
print(anEdge.Length)

Теперь вы получить доступ ко всем свойствам ребра, с помощью длинны или позиции. Это означает, что у ребра в 100mm длинной, начальная позиция это 0 а конечная это 100.

anEdge.tangentAt(0.0)          # tangent direction at the beginning
anEdge.valueAt(0.0)            # Point at the beginning
anEdge.valueAt(100.0)          # Point at the end of the edge
anEdge.derivative1At(50.0)     # first derivative of the curve in the middle
anEdge.derivative2At(50.0)     # second derivative of the curve in the middle
anEdge.derivative3At(50.0)     # third derivative of the curve in the middle
anEdge.centerOfCurvatureAt(50) # center of the curvature for that position
anEdge.curvatureAt(50.0)       # the curvature
anEdge.normalAt(50)            # normal vector at that position (if defined)

Использование выделения(выбора)

Здесь мы увидим как можно использовать "выделение", которое пользователь сделал в программе просмотра. прежде всего мы создадим блок и отобразим его в окне просмотра.

Here we see now how we can use a selection the user did in the viewer. First of all we create a box and show it in the viewer.

import Part
Part.show(Part.makeBox(100, 100, 100))
Gui.SendMsgToActiveView("ViewFit")

Теперь выберем грани или ребра. С помощью этого сценария вы можете повторить по всем выделенным объектам и их субэлементам:

for o in Gui.Selection.getSelectionEx():
    print(o.ObjectName)
    for s in o.SubElementNames:
        print("name: ", s)
        for s in o.SubObjects:
            print("object: ", s)

Выделим несколько ребер и этот сценарий подсчитает их сумарную длину:

length = 0.0
for o in Gui.Selection.getSelectionEx():
    for s in o.SubObjects:
        length += s.Length

print("Length of the selected edges: ", length)

Полный пример: бутыль OCC

Типовой пример, взятый на OpenCasCade Technology Tutorial - это как построить бутыль. Это отличный пример и для FreeCAD. В самом деле, если последуете нашему примеру изложенному ниже и странице OCC одновременно, вы лучше поймете как структуры OCC реализованы в FreeCAD. Готовый сценарий описанный ниже, также включен в установленный FreeCAD (в папке Mod/Part) и может быть вызван интерпретатором python, вводом:

A typical example found on the OpenCasCade Technology website is how to build a bottle. This is a good exercise for FreeCAD too. In fact, if you follow our example below and the OCC page simultaneously, you will see how well OCC structures are implemented in FreeCAD. The script is included in the FreeCAD installation (inside the Mod/Part folder) and can be called from the Python interpreter by typing:

import Part
import MakeBottle
bottle = MakeBottle.makeBottle()
Part.show(bottle)

Готовый сценарий

Здесь представлен готовый сценарий MakeBottle:

For the purpose of this tutorial we will consider a reduced version of the script. In this version the bottle will not be hollowed out, and the neck of the bottle will not be threaded.

import FreeCAD as App
import Part, math

def makeBottleTut(myWidth = 50.0, myHeight = 70.0, myThickness = 30.0):
    aPnt1=App.Vector(-myWidth / 2., 0, 0)
    aPnt2=App.Vector(-myWidth / 2., -myThickness / 4., 0)
    aPnt3=App.Vector(0, -myThickness / 2., 0)
    aPnt4=App.Vector(myWidth / 2., -myThickness / 4., 0)
    aPnt5=App.Vector(myWidth / 2., 0, 0)

    aArcOfCircle = Part.Arc(aPnt2, aPnt3, aPnt4)
    aSegment1=Part.LineSegment(aPnt1, aPnt2)
    aSegment2=Part.LineSegment(aPnt4, aPnt5)

    aEdge1=aSegment1.toShape()
    aEdge2=aArcOfCircle.toShape()
    aEdge3=aSegment2.toShape()
    aWire=Part.Wire([aEdge1, aEdge2, aEdge3])

    aTrsf=App.Matrix()
    aTrsf.rotateZ(math.pi) # rotate around the z-axis

    aMirroredWire=aWire.copy()
    aMirroredWire.transformShape(aTrsf)
    myWireProfile=Part.Wire([aWire, aMirroredWire])

    myFaceProfile=Part.Face(myWireProfile)
    aPrismVec=App.Vector(0, 0, myHeight)
    myBody=myFaceProfile.extrude(aPrismVec)

    myBody=myBody.makeFillet(myThickness / 12.0, myBody.Edges)

    neckLocation=App.Vector(0, 0, myHeight)
    neckNormal=App.Vector(0, 0, 1)

    myNeckRadius = myThickness / 4.
    myNeckHeight = myHeight / 10.
    myNeck = Part.makeCylinder(myNeckRadius, myNeckHeight, neckLocation, neckNormal)
    myBody = myBody.fuse(myNeck)

    return myBody

el = makeBottleTut()
Part.show(el)

Подробные объяснения

import FreeCAD as App
import Part, math

Нам, конечно, необходимы модуль Part, а также модуль FreeCAD.Base, который содержит основные структуры FreeCAD, такие как векторы и матрицы.

def makeBottleTut(myWidth = 50.0, myHeight = 70.0, myThickness = 30.0):
    aPnt1=App.Vector(-myWidth / 2., 0, 0)
    aPnt2=App.Vector(-myWidth / 2., -myThickness / 4., 0)
    aPnt3=App.Vector(0, -myThickness / 2., 0)
    aPnt4=App.Vector(myWidth / 2., -myThickness / 4., 0)
    aPnt5=App.Vector(myWidth / 2., 0, 0)

Здесь мы задаем нашу функцию makeBottleTut. Эта функция может быть вызвана без аргументов, как мы делали выше, в этом случае будут использоваться значения по умолчанию для ширины, высоты и толщины. Затем мы определили несколько точек которые будут использоваться для построения базового сечения.

...
    aArcOfCircle = Part.Arc(aPnt2, aPnt3, aPnt4)
    aSegment1=Part.LineSegment(aPnt1, aPnt2)
    aSegment2=Part.LineSegment(aPnt4, aPnt5)

Здесь мы задаём геометрию: дугу, созданую по 3 точкам, и два линейных сегмента, созданные по 2 точкам.

...
    aEdge1=aSegment1.toShape()
    aEdge2=aArcOfCircle.toShape()
    aEdge3=aSegment2.toShape()
    aWire=Part.Wire([aEdge1, aEdge2, aEdge3])

Запомнили различие между геометрией и формой? Здесь мы создаем форму из нашей строительной геометрии. Три рёбра (ребра могут быть прямыми или кривыми), затем из этих трёх рёбер создается ломанная.

...
    aTrsf=App.Matrix()
    aTrsf.rotateZ(math.pi) # rotate around the z-axis

    aMirroredWire=aWire.copy()
    aMirroredWire.transformShape(aTrsf)
    myWireProfile=Part.Wire([aWire, aMirroredWire])

Пока мы построили только половину сечения. Вместо построения таким же образом целого профиля, мы можем просто отразить то, что мы сделали, и склеить две половинки. Сначала создадим матрицу. Матрица является распространенным способом произвести изменения над объектом в трёхмерном пространстве, поскольку она может содержать в одной структуре все базовые преобразования, которым могут подвергаться трёхмерные объекты (перемещение, вращение и масштабирование). После создания матрицы, мы отражаем её, затем создаем копию нашей ломанной и применяем к ней трансформационную матрицу. Теперь мы получили две ломанные и мы можем создать из них третью ломаную, так как ломанные это всего лишь список ребер.

...
    myFaceProfile=Part.Face(myWireProfile)
    aPrismVec=App.Vector(0, 0, myHeight)
    myBody=myFaceProfile.extrude(aPrismVec)

    myBody=myBody.makeFillet(myThickness / 12.0, myBody.Edges)

Теперь мы получили замкнутую ломаную, которую можно обратить в грань. Когда мы имеем грань, мы можем вытянуть её. Сделав это, мы получим твердое тело. Теперь мы добавим небольшое скругление к нашему объекту, потому что мы заботимся о качественном дизайне, не так ли?

...
    neckLocation=App.Vector(0, 0, myHeight)
    neckNormal=App.Vector(0, 0, 1)

    myNeckRadius = myThickness / 4.
    myNeckHeight = myHeight / 10.
    myNeck = Part.makeCylinder(myNeckRadius, myNeckHeight, neckLocation, neckNormal)

Теперь тело нашей бутыли создано, но нам нужно создать горлышко. Так что мы создаем новое твердое тело, с цилиндром.

...
    myBody = myBody.fuse(myNeck)

Операция слияния очень мощная. Она заботится о склеивании, о том, что должно быть приклеено и удаляет части, которые следует удалить.

...
    return myBody

Теперь мы получаем нашу твёрдое тело модуля Part как результат нашей функции.

el = makeBottleTut()
Part.show(el)

В итоге мы вызываем функцию для фактического создания детали, а потом делаем её видимой.

Example: Pierced box

Here is a complete example of building a pierced box.

Конструкция делается по одной стороне за раз. Когда куб закончен, он выдалбливается вырезанием цилиндра через него.

import FreeCAD as App
import Part, math

size = 10
poly = Part.makePolygon([(0, 0, 0), (size, 0, 0), (size, 0, size), (0, 0, size), (0, 0, 0)])

face1 = Part.Face(poly)
face2 = Part.Face(poly)
face3 = Part.Face(poly)
face4 = Part.Face(poly)
face5 = Part.Face(poly)
face6 = Part.Face(poly)
     
myMat = App.Matrix()

myMat.rotateZ(math.pi / 2)
face2.transformShape(myMat)
face2.translate(App.Vector(size, 0, 0))

myMat.rotateZ(math.pi / 2)
face3.transformShape(myMat)
face3.translate(App.Vector(size, size, 0))

myMat.rotateZ(math.pi / 2)
face4.transformShape(myMat)
face4.translate(App.Vector(0, size, 0))

myMat = App.Matrix()

myMat.rotateX(-math.pi / 2)
face5.transformShape(myMat)

face6.transformShape(myMat)               
face6.translate(App.Vector(0, 0, size))

myShell = Part.makeShell([face1, face2, face3, face4, face5, face6])   
mySolid = Part.makeSolid(myShell)

myCyl = Part.makeCylinder(2, 20)
myCyl.translate(App.Vector(size / 2, size / 2, 0))

cut_part = mySolid.cut(myCyl)

Part.show(cut_part)

Загрузка и Сохранение

Существует несколько способов сохранить вашу работу. Вы конечно можете сохранить ваш FreeCAD документ, а также вы можете сохранить Part(Деталь) объект напрямую в обычные CAD форматы, такие как BREP, IGS, STEP и STL.

Сохранить форму в файл легко. Есть доступные для всех форм методы exportBrep(), exportIges(), exportStep() и exportStl(). Таким образом:

import Part
s = Part.makeBox(10, 10, 10)
s.exportStep("test.stp")

это сохранит наш блок в файл формата STEP. Для загрузки BREP, IGES или STEP файлов:

import Part
s = Part.Shape()
s.read("test.stp")

Для преобразования файла STEP в файл IGS:

import Part
 s = Part.Shape()
 s.read("file.stp")       # incoming file igs, stp, stl, brep
 s.exportIges("file.igs") # outbound file igs

FreeCAD Scripting Basics

Оглавление

Power user documentation

FreeCAD scripting: Python, Introduction to Python, Python scripting tutorial, FreeCAD Scripting Basics

Modules: Builtin modules, Units, Quantity
Workbenches: Workbench creation, Gui Commands, Commands, Installing more workbenches
Meshes and Parts: Mesh Scripting, Topological data scripting, Mesh to Part, PythonOCC

Parametric objects: Scripted objects, Viewproviders (Custom icon in tree view)
Scenegraph: Coin (Inventor) scenegraph, Pivy
Graphical interface: Interface creation, Interface creation completely in Python (1, 2, 3, 4, 5), PySide, PySide examples beginner, intermediate, advanced
Macros: Macros, How to install macros
Embedding: Embedding FreeCAD, Embedding FreeCADGui

Other: Expressions, Code snippets, Line drawing function, FreeCAD vector math library (deprecated)

Hubs: User hub, Power users hub, Developer hub