Macro Draft Circle 3 Points 3D/de

Draft Kreis aus drei Punkten 3D
Beschreibung
Dieses Makro erstellt einen Kreis an drei ausgewählten Punkten im Raum. Die Punkte können Objekte wie Würfel oder Zylinder sein, dann sind die ausgewählten Koordinaten der Mittelpunkt dieser Formen. Versionsmakro : 01.00 Datum der letzten Änderung : 2013-03-16 FreeCAD version : Alle Herunterladen : Werkzeugleisten-Symbol Autor: galou_breizh
Autor
galou_breizh
Herunterladen
Werkzeugleisten-Symbol
Links
Makros Rezepte Wie man Makros installiert Symbolleisten anpassen
Macro-Version
01.00
Datum der letzten Änderung
2013-03-16
FreeCAD-Version(s)
Alle
Standardverknüpfung
None
Siehe auch
None

Beschreibung

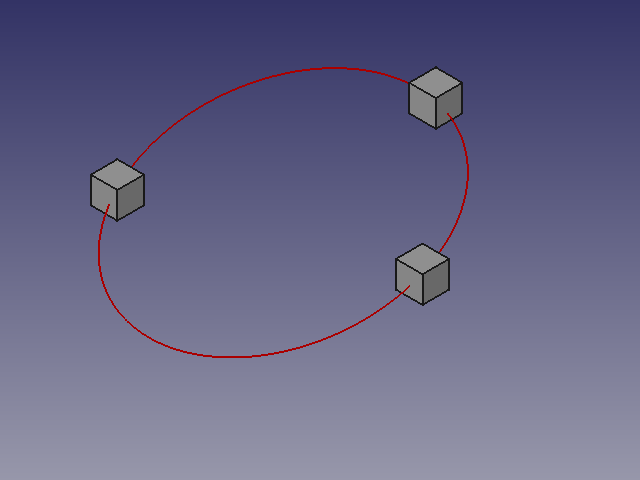
Dieses Makro erstellt einen Kreis durch drei ausgewählte Punkte im Raum. Die Punkte können Objekte wie Würfel oder Zylinder sein. Die ausgewählten Koordinaten bilden dann den Mittelpunkt dieser Formen.

Anwendung

Drei Punkte oder Formen in der 3D-Ansicht auswählen und das Makro ausführen.
Wenn die Form eine Linie ist, wird die Koordinate der Mittelpunkt der Linie sein.

Einschränkungen

Die Reihenfolge der Auswahl der Angstformen beeinflusst den AXIS-Winkel und kehrt die Neigung des Kreises um. In diesem Fall können Sie die Reihenfolge der Auswahl der Formen umkehren oder ändern.
Die Koordinaten X, Y, Z des Werts 0 oder die Ausrichtung, die keine Berechnung zulässt, können eine Division durch einen Null-Fehler zurückgeben und mit "Die drei Punkte sind ausgerichtet" übersetzt.

Skript

Werkzeugleistensymbol

Macro_Draft_Circle_3_Points_3D.FCMacro

# -*- coding: utf-8 -*-
# Create a circle from 3 points selected on the X, Y, Z map
# 04/03/2013
# From https://en.wikipedia.org/wiki/Circumscribed_circle#Cartesian_coordinates_from_cross-_and_dot-products
# Also see : https://math.stackexchange.com/questions/2658318/how-to-find-the-circumcenter-of-a-triangle-and-the-length-of-the-corresponding-r
# O=R/2S*(acosα⋅A+bcosβ⋅B+ccosγ⋅C)  ; R is circumradius, S is area of triangle
# 08/08/2014 PyQt4 and PySide

#OS: Windows Vista
#Word size: 32-bit
#Version: 0.14.3700 (Git)
#Branch: releases/FreeCAD-0-14
#Hash: 32f5aae0a64333ec8d5d160dbc46e690510c8fe1
#Python version: 2.6.2
#Qt version: 4.5.2
#Coin version: 3.1.0
#SoQt version: 1.4.1
#OCC version: 6.5.1

try:
    import PyQt4
    from PyQt4 import QtCore, QtGui
except Exception:
    import PySide
    from PySide import QtCore, QtGui
from math import pi, asin
import Draft, FreeCAD, FreeCADGui
from FreeCAD import Base

def errorDialog(msg):
    # Create a simple dialog QMessageBox
    # The first argument indicates the icon used: one of QtGui.QMessageBox.{NoIcon, Information, Warning, Critical, Question} 
    diag = QtGui.QMessageBox(QtGui.QMessageBox.Critical,u"Error Message",msg)
    diag.setWindowModality(QtCore.Qt.ApplicationModal)
    diag.exec_()

def affiche(x,y,z,r,angle):
    diag = QtGui.QMessageBox(QtGui.QMessageBox.Information,u"Coordinates",u"Coordinate X : "+str(x)+"\r\n"+u"Coordinate Y : "+str(y)+"\n"+u"Coordinate Z : "+str(z)+"\nRadius\t   : "+str(r)+"\nAngle\t   : "+str(angle))
    diag.setWindowModality(QtCore.Qt.ApplicationModal)
    diag.setWindowModality(QtCore.Qt.NonModal)
    diag.exec_()

# objects selected
sel = FreeCADGui.Selection.getSelection()
# If there are 3 selected points so...
if len(sel)==3 :
    # Assignment of variables
    P1 = sel[0].Shape.BoundBox.Center
    P2 = sel[1].Shape.BoundBox.Center
    P3 = sel[2].Shape.BoundBox.Center

    P1P2 = (P2 - P1).Length
    P2P3 = (P3 - P2).Length
    P3P1 = (P1 - P3).Length

    # Circle radius.
    l = ((P1 - P2).cross(P2 - P3)).Length
    try:
        #if l < 1e-8:
        #    errorDialog("The three points are aligned")
        r = P1P2 * P2P3 * P3P1 / 2 / l
    except:
        errorDialog("The three points are aligned")
    else:
        # Sphere center.
        a = P2P3**2 * (P1 - P2).dot(P1 - P3) / 2 / l**2
        b = P3P1**2 * (P2 - P1).dot(P2 - P3) / 2 / l**2
        c = P1P2**2 * (P3 - P1).dot(P3 - P2) / 2 / l**2
        P1.multiply(a)
        P2.multiply(b)
        P3.multiply(c)
        PC = P1 + P2 + P3

        # Creation of a circle
        pl = Base.Placement()
        v = (P1 - P2).cross(P3 - P2)
        v.normalize()
        axis = Base.Vector(0, 0, 1).cross(v)
        angle = asin(axis.Length) * 180 / pi
        axis.normalize()
        pl = Base.Placement(PC, axis, angle)
        Draft.makeCircle(r, placement=pl, face=False, support=None)
        # Displays the result in the windows
        affiche((PC.x),(PC.y),(PC.z),r,angle)
        # Displays the result in the FreeCAD report view
        #FreeCAD.Console.PrintMessage("Coordinate X : "+str(PC.x)+"\n")
        #FreeCAD.Console.PrintMessage("Coordinate Y : "+str(PC.y)+"\n")
        #FreeCAD.Console.PrintMessage("Coordinate Z : "+str(PC.z)+"\n")
        #FreeCAD.Console.PrintMessage("Radius       : "+str(r)+"\n")
        #FreeCAD.Console.PrintMessage("Angle        : "+str(angle)+"\n")
else:
    # If the condition is not met, repeat
    #FreeCAD.Console.PrintError("Select 3 points and repeat\n")
    errorDialog("Select 3 points and repeat\n")