Topological data scripting/fr
Introduction
Nous allons vous expliquer ici comment contrôler le module Part directement à partir de l'interpréteur Python de FreeCAD ou depuis n'importe quel script externe. N'hésitez pas à consulter les pages des scripts et les bases pour script dans Freecad si vous avez besoin de plus d'informations sur le fonctionnement des scripts Python dans FreeCAD. Si vous débutez avec Python, il est recommandé de commencer par lire la page Introduction à Python.
Voir aussi
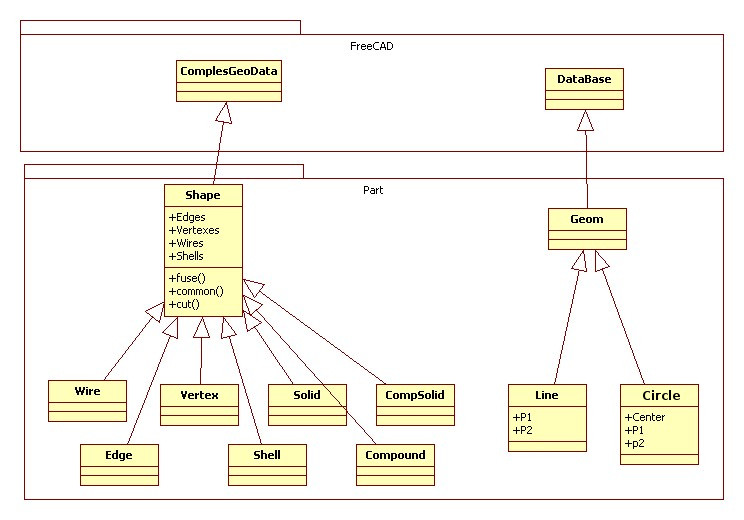
Diagramme de classe
Voici un aperçu du Langage de Modélisation Unifié (UML) de la classe la plus importante du module Part :
Géométrie
Les objets géométriques sont les éléments constitutifs de tous les objets topologiques :
- Geom Classe de base des objets géométriques.
- Ligne Une ligne droite en 3D, définie par le point de départ et le point d'arrivée.
- Cercle Cercle ou arc de cercle, défini par un centre, un point de départ et d'arrivée.
- Etc...
Topologie
Les types de données topologiques suivants sont disponibles :
- Composé Un groupe de tout type d'objets topologiques.
- Compsolid Un solide composite est un ensemble de solides reliés par leurs faces. Il étend les notions de FORME FILAIRE et de COQUE aux solides.
- Solide Une partie de l'espace limité par des coques. C'est en trois dimensions.
- Coque Un ensemble de faces reliées par leurs arrêtes. Une coque peut être ouverte ou fermée.
- Face En 2D, elle fait partie d'un plan ; en 3D elle fait partie d'une surface. Sa géométrie est contrainte (rognée) par des contours. C'est bidimensionnel.
- Forme filaire Un ensemble d'arêtes reliées par leurs sommets. Il peut s'agir d'un contour ouvert ou fermé selon que les bords sont liés ou non.
- Arête Un élément topologique correspondant à une courbe restreinte. Une arête est généralement limitée par des sommets. Elle a une dimension.
- Sommet Un élément topologique correspondant à un point. Il a une dimension nulle.
- Forme Terme générique couvrant tout ce qui précède.
Exemple rapide : Création topologique simple
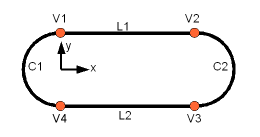
Nous allons maintenant créer une topologie, en la construisant à partir d'une géométrie plus simple. Comme étude de cas, nous utiliserons une ensemble comme illustré ci-dessus, qui se compose de quatre sommets, deux arcs et deux lignes.
Création de la géométrie
Nous créons d'abord les parties géométriques distinctes de ce fil. S'assurer que les éléments qui doivent être connectées ultérieurement partagent les mêmes sommets.
Donc, nous créons d'abord les sommets :
import FreeCAD as App
import Part
V1 = App.Vector(0, 10, 0)
V2 = App.Vector(30, 10, 0)
V3 = App.Vector(30, -10, 0)
V4 = App.Vector(0, -10, 0)
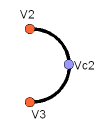
Arc
Pour chaque arc, nous avons besoin d'un point de repère :
VC1 = App.Vector(-10, 0, 0)
C1 = Part.Arc(V1, VC1, V4)
VC2 = App.Vector(40, 0, 0)
C2 = Part.Arc(V2, VC2, V3)
Ligne
Les segments de ligne peuvent être créés à partir de deux points :
L1 = Part.LineSegment(V1, V2)
L2 = Part.LineSegment(V3, V4)
Relier le tout
La dernière étape consiste à assembler les éléments géométriques de base et façonner une forme topologique :
S1 = Part.Shape([C1, L1, C2, L2])
Construire un prisme
Maintenant, extrudez la forme filaire dans une direction et créez une forme 3D véritable :
W = Part.Wire(S1.Edges)
P = W.extrude(App.Vector(0, 0, 10))
Affichons le tout
Part.show(P)
Création de formes basiques
Vous pouvez facilement créer des objets topologiques de base avec les méthodes make...() de l'atelier Part :
b = Part.makeBox(100, 100, 100)
Part.show(b)
Quelques méthodes make...() disponibles :
makeBox(l, w, h, [p, d])Crée une boîte située en p et pointant dans la direction d avec les dimensions longueur, largeur et hauteur.makeCircle(radius)Dessine un cercle avec un rayon donné.makeCone(radius1, radius2, height)Crée un cône avec rayons1, rayon2 et hauteur donnés.makeCylinder(radius, height)Crée un cylindre avec un rayon et une hauteur donnés.makeLine((x1, y1, z1), (x2, y2, z2))Trace un segment à partir de deux points.makePlane(length, width)Crée un plan avec la longueur et la largeur.makePolygon(list)Crée un polygone à partir d'une liste de points.makeSphere(radius)Crée une sphère avec un rayon donné.makeTorus(radius1, radius2)Crée un tore avec les rayons donnés.
Voir la page de l'API Part ou cette documentation autogénérée de l'API Python de Part pour une liste complète des méthodes disponibles du module Part.
Importer les modules nécessaires
Tout d'abord, nous devons importer les modules FreeCAD et Part afin de pouvoir utiliser leur contenu en Python :
import FreeCAD as App
import Part
Création d'un vecteur
Les vecteurs constituent l'une des informations les plus importantes, lors de la construction des formes géométriques. Ils contiennent généralement trois nombres (mais pas systématiquement) : les coordonnées cartésiennes X, Y et Z. Vous créer un vecteur comme ceci :
myVector = App.Vector(3, 2, 0)
Nous venons de créer un vecteur aux coordonnées X=3, Y=2, Z=0. Dans le module Part, les vecteurs sont utilisés partout. Part shapes utilise également un autre type de représentation ponctuelle appelée sommet, qui est simplement un conteneur pour un vecteur. Vous accédez au vecteur d'un sommet comme ceci :
myVertex = myShape.Vertexes[0]
print(myVertex.Point)
> Vector (3, 2, 0)
Création d'une arête
Une arête n'est rien d'autre qu'un segment avec deux sommets :
edge = Part.makeLine((0, 0, 0), (10, 0, 0))
edge.Vertexes
> [<Vertex object at 01877430>, <Vertex object at 014888E0>]
Remarque : Vous pouvez également créer une arête en passant deux vecteurs :
vec1 = App.Vector(0, 0, 0)
vec2 = App.Vector(10, 0, 0)
line = Part.LineSegment(vec1, vec2)
edge = line.toShape()
Vous pouvez trouver la longueur et le centre d'une arête comme ceci :
edge.Length
> 10.0
edge.CenterOfMass
> Vector (5, 0, 0)
Mise en forme à l'écran
Jusqu'à présent, nous avons créé un objet filaire, mais il n'apparaît nulle part à l'écran. En effet, la scène FreeCAD 3D affiche uniquement ce que vous lui demandez d'afficher. Pour ce faire, nous utilisons cette simple méthode :
Part.show(edge)
La fonction show crée un objet dans notre document FreeCAD et lui assigne notre forme "filaire". Utilisez-la chaque fois qu'il est temps d'afficher votre création à l'écran.
Création d'un contour (ou forme filaire)
Un contour est une polyligne, à arêtes multiples et peut être créé à partir d'une liste d'arêtes ou même une liste de contours (ou de formes filaires) :
edge1 = Part.makeLine((0, 0, 0), (10, 0, 0))
edge2 = Part.makeLine((10, 0, 0), (10, 10, 0))
wire1 = Part.Wire([edge1, edge2])
edge3 = Part.makeLine((10, 10, 0), (0, 10, 0))
edge4 = Part.makeLine((0, 10, 0), (0, 0, 0))
wire2 = Part.Wire([edge3, edge4])
wire3 = Part.Wire([wire1, wire2])
wire3.Edges
> [<Edge object at 016695F8>, <Edge object at 0197AED8>, <Edge object at 01828B20>, <Edge object at 0190A788>]
Part.show(wire3)
Part.show(wire3) affichera les 4 bords qui composent notre forme filaire. D'autres informations utiles peuvent être facilement récupérées :
wire3.Length
> 40.0
wire3.CenterOfMass
> Vector (5, 5, 0)
wire3.isClosed()
> True
wire2.isClosed()
> False
Création d'une face
Seules les faces créées à partir de formes filaires fermées seront valides. Dans cet exemple, wire3 est un contour fermé mais wire2 ne l'est pas (voir ci-dessus) :
face = Part.Face(wire3)
face.Area
> 99.99999999999999
face.CenterOfMass
> Vector (5, 5, 0)
face.Length
> 40.0
face.isValid()
> True
sface = Part.Face(wire2)
sface.isValid()
> False
Seules les faces auront une superficie, mais pas les contours et les arêtes.
Création d'un cercle
Un cercle peut être créé comme ceci :
circle = Part.makeCircle(10)
circle.Curve
> Circle (Radius : 10, Position : (0, 0, 0), Direction : (0, 0, 1))
Si vous voulez le créer à une certaine position et avec une certaine direction :
ccircle = Part.makeCircle(10, App.Vector(10, 0, 0), App.Vector(1, 0, 0))
ccircle.Curve
> Circle (Radius : 10, Position : (10, 0, 0), Direction : (1, 0, 0))
ccircle sera créé à la distance 10 de l'origine X et sera orienté vers l'extérieur le long de l'axe X. Remarque : makeCircle() n'accepte que App.Vector() pour les paramètres position et les paramètres normaux, et non les tuples. Vous pouvez également créer une partie du cercle en donnant un angle de départ et un angle d'arrivée :
from math import pi
arc1 = Part.makeCircle(10, App.Vector(0, 0, 0), App.Vector(0, 0, 1), 0, 180)
arc2 = Part.makeCircle(10, App.Vector(0, 0, 0), App.Vector(0, 0, 1), 180, 360)
Les angles doivent être renseignés en degrés. Si vous avez des radians, convertissez-les simplement en utilisant la formule : degrés = radians * 180/pi ou en utilisant le module math de Python :
import math
degrees = math.degrees(radians)
Création d'un arc avec des points (repères)
Malheureusement, il n'y a pas de fonction makeArc(), mais nous avons la fonction Part.Arc() pour créer un arc de cercle passant par trois points. Il crée un objet arc, joignant le point de départ au point d'arrivée, en passant par le point médian. La fonction toShape() de l'objet arc, doit être appelée pour obtenir un objet filaire, comme lorsque vous utilisez Part.LineSegment au lieu de Part.makeLine.
arc = Part.Arc(App.Vector(0, 0, 0), App.Vector(0, 5, 0), App.Vector(5, 5, 0))
arc
> <Arc object>
arc_edge = arc.toShape()
Part.show(arc_edge)
Arc() n'accepte que App.Vector() pour les points et non les tuples. Vous pouvez également obtenir un arc en utilisant une partie d'un cercle :
from math import pi
circle = Part.Circle(App.Vector(0, 0, 0), App.Vector(0, 0, 1), 10)
arc = Part.Arc(circle,0,pi)
Les arcs sont des arêtes valides comme les segments, ils peuvent donc également être utilisés dans les contours (ou forme filaire).
Création de polygones
Un polygone est simplement une forme filaire, avec plusieurs bords droits. La fonction makePolygon() prend une liste de points et crée un contour, passant à travers ces points :
lshape_wire = Part.makePolygon([App.Vector(0, 5, 0), App.Vector(0, 0, 0), App.Vector(5, 0, 0)])
Création de courbes de Bézier
Les courbes de Bézier sont utilisées, pour modéliser des courbes lisses à l'aide d'une série de points de contrôle et de poids facultatifs. La fonction ci-dessous crée un Part.BezierCurve(), à partir d'une série de points FreeCAD.Vector(). Remarque : lors de "l'obtention" et du "réglage" d'un seul pôle ou poids, les indices commencent à 1, pas à 0.
def makeBCurveEdge(Points):
geomCurve = Part.BezierCurve()
geomCurve.setPoles(Points)
edge = Part.Edge(geomCurve)
return(edge)
Création d'un plan
Un plan est une surface rectangulaire plate. La méthode utilisée pour le créer est makePlane(length, width, [start_pnt, dir_normal]). Par défaut start_pnt = Vector(0, 0, 0) et dir_normal = Vector(0, 0, 1). L'utilisation de dir_normal = Vector(0, 0, 1) créera le plan orienté dans la direction positive de l'axe Z, tandis que dir_normal = Vector(1, 0, 0) créera le plan orienté dans la direction positive de l'axe X :
plane = Part.makePlane(2, 2)
plane
> <Face object at 028AF990>
plane = Part.makePlane(2, 2, App.Vector(3, 0, 0), App.Vector(0, 1, 0))
plane.BoundBox
> BoundBox (3, 0, 0, 5, 0, 2)
BoundBox est un cuboïde entourant le plan avec une diagonale commençant à (3, 0, 0) et se terminant en (5, 0, 2). Ici, l'épaisseur du BoundBox le long de l'axe Y est nulle, puisque notre forme est totalement plate.
Remarque : makePlane() accepte uniquement App.Vector() pour start_pnt et dir_normal et pas les tuples.
Création d'une ellipse
Il existe plusieurs façons de créer une ellipse :
Part.Ellipse()
Crée une ellipse avec un grand rayon de 2 et un petit rayon de 1 avec le centre à (0, 0, 0).
Part.Ellipse(Ellipse)
Crée une copie de l'ellipse donnée.
Part.Ellipse(S1, S2, Center)
Crée une ellipse centrée sur le point Centre, où le plan de l'ellipse est défini par Center, S1 et S2, son grand axe est défini par Center et S1, son grand rayon est la distance entre Center et S1 et son petit rayon est la distance entre S2 et le grand axe.
Part.Ellipse(Center, MajorRadius, MinorRadius)
Crée une ellipse avec un grand rayon MajorRadius et un petit rayon MinorRadius, situé dans le plan défini par le Centre et la normale (0, 0, 1).
eli = Part.Ellipse(App.Vector(10, 0, 0), App.Vector(0, 5, 0), App.Vector(0, 0, 0))
Part.show(eli.toShape())
Dans le code ci-dessus, nous avons passé S1, S2 et le centre. De même que l'Arc, l'Ellipse crée un objet ellipse et non une arête, nous devons donc le convertir en arête en utilisant toShape() pour l'affichage.
Remarque : Ellipse() n'accepte que App.Vector() pour les points et pas les tuples.
eli = Part.Ellipse(App.Vector(0, 0, 0), 10, 5)
Part.show(eli.toShape())
Pour construire l'Ellipse ci-dessus, nous avons entré les coordonnées centrales, le Grand rayon et le Petit rayon.
Création d'un tore
Utilisation de makeTorus(radius1, radius2, [pnt, dir, angle1, angle2, angle]). Par défaut pnt = Vector (0, 0, 0), dir = Vector (0, 0, 1), angle1 = 0, angle2 = 360 et angle = 360. Considérez un tore comme un petit cercle balayant un grand cercle. Radius1 est le rayon du grand cercle, radius2 est le rayon du petit cercle, pnt est le centre du tore et dir est la direction normale. Angle1 et angle2 sont des angles en degrés pour le petit cercle; le dernier paramètre d'angle est la section du tore :
torus = Part.makeTorus(10, 2)
Le code ci-dessus créera un tore avec un diamètre de 20 (rayon de 10) et une épaisseur de 4 (rayon du petite cercle 2).
tor=Part.makeTorus(10, 5, App.Vector(0, 0, 0), App.Vector(0, 0, 1), 0, 180)
Le code ci-dessus créera une portion du tore.
tor=Part.makeTorus(10, 5, App.Vector(0, 0, 0), App.Vector(0, 0, 1), 0, 360, 180)
Le code ci-dessus créera un semi-tore ; seul le dernier paramètre est modifié, c'est-à-dire que les angles restants sont des valeurs par défaut. Attribuer l'angle 180 créera le tore de 0 à 180, c'est-à-dire un demi tore.
Création d'un pavé ou d'un cuboïde
Utilisez makeBox(length, width, height, [pnt, dir]).
Par défaut pnt = Vector(0, 0, 0) et dir = Vector(0, 0, 1).
box = Part.makeBox(10, 10, 10)
len(box.Vertexes)
> 8
Création d'une sphère
Utilisation de makeSphere(radius, [pnt, dir, angle1, angle2, angle3]). Par défaut pnt = Vector(0, 0, 0), dir = Vector(0, 0, 1), angle1 = -90, angle2 = 90 et angle3 = 360. Angle1 et angle2 correspondent au minimum et au maximum vertical de la sphère, angle3 est le diamètre de la sphère.
sphere = Part.makeSphere(10)
hemisphere = Part.makeSphere(10, App.Vector(0, 0, 0), App.Vector(0, 0, 1), -90, 90, 180)
Création d'un cylindre
Nous utiliserons makeCylinder(radius, height, [pnt, dir, angle]). Par défaut, pnt = Vector(0, 0, 0), dir = Vector(0, 0, 1) et angle = 360.
cylinder = Part.makeCylinder(5, 20)
partCylinder = Part.makeCylinder(5, 20, App.Vector(20, 0, 0), App.Vector(0, 0, 1), 180)
Création d'un cône
Nous utiliserons makeCone(radius1, radius2, height, [pnt, dir, angle]). Par défaut, pnt = Vector(0, 0, 0), dir = Vector(0, 0, 1) et angle = 360.
cone = Part.makeCone(10, 0, 20)
semicone = Part.makeCone(10, 0, 20, App.Vector(20, 0, 0), App.Vector(0, 0, 1), 180)
Modification d'une forme
Il y a plusieurs manières de modifier des formes. Certaines sont de simples opérations de transformation telles que le déplacement ou la rotation de formes, d'autres sont plus complexes telles que fusion et soustraction d'une forme à une autre.
Opérations de transformation
Transformer une forme
La transformation est l'action de déplacer une forme d'un endroit à un autre. Toute forme (arête, face, cube, etc ...) peut être transformée de la même manière :
myShape = Part.makeBox(2, 2, 2)
myShape.translate(App.Vector(2, 0, 0))
Cette commande va déplacer notre forme "myShape" de 2 unités dans la direction X.
Rotation d'une forme
Pour faire pivoter une forme, vous devez spécifier le centre de rotation, l'axe et l'angle de rotation :
myShape.rotate(App.Vector(0, 0, 0),App.Vector(0, 0, 1), 180)
Cette opération va faire pivoter notre forme de 180 degrés sur l'axe z.
Transformations génériques avec matrices
Une matrice est un moyen très simple de mémoriser les transformations dans le mode 3D. Dans une seule matrice, vous pouvez définir les valeurs de transformation, rotation et mise à l'échelle à appliquer à un objet. Par exemple :
myMat = App.Matrix()
myMat.move(App.Vector(2, 0, 0))
myMat.rotateZ(math.pi/2)
PS: les matrices de FreeCAD travaillent en radians. En outre presque toutes les opérations matricielles qui travaillent avec un vecteur peuvent aussi avoir 3 nombres de sorte que ces 2 lignes effectuent le même travail :
myMat.move(2, 0, 0)
myMat.move(App.Vector(2, 0, 0))
Lorsque notre matrice est paramétrée, nous pouvons l'appliquer à notre forme. FreeCAD fournit nous fournit 2 méthodes : transformShape() et transformGeometry(). La différence est que, avec la première, vous ne verez pas de différence (voir Mettre à l'échelle une forme ci-dessous). Donc, nous pouvons opérer notre transformation comme ceci :
myShape.transformShape(myMat)
ou
myShape.transformGeometry(myMat)
Mettre à l'échelle une forme
La mise à l'échelle d'une forme est une opération plus dangereuse car, contrairement à la traduction ou rotation, mise à l'échelle non uniforme (avec des valeurs différentes pour X, Y et Z) peut modifier la structure de la forme. Par exemple, mettre à l'échelle un cercle avec une valeur plus élevée horizontalement que verticalement le transformera en un ellipse, qui se comporte mathématiquement très différemment. Pour la mise à l'échelle, nous ne peut pas utiliser transformShape(), nous devons utiliser transformGeometry() :
myMat = App.Matrix()
myMat.scale(2, 1, 1)
myShape=myShape.transformGeometry(myMat)
Opérations Booléennes
Soustraction
Soustraire une forme d'une autre est appelé, dans le jargon de FreeCAD "cut" (coupe) et se fait de cette manière :
cylinder = Part.makeCylinder(3, 10, App.Vector(0, 0, 0), App.Vector(1, 0, 0))
sphere = Part.makeSphere(5, App.Vector(5, 0, 0))
diff = cylinder.cut(sphere)
Intersection
De la même manière, l'intersection entre 2 formes est appelé "common" (commun) et se fait de cette manière :
cylinder1 = Part.makeCylinder(3, 10, App.Vector(0, 0, 0), App.Vector(1, 0, 0))
cylinder2 = Part.makeCylinder(3, 10, App.Vector(5, 0, -5), App.Vector(0, 0, 1))
common = cylinder1.common(cylinder2)
Fusion
L'union est appelé "fuse" (fusion) et fonctionne de la même manière :
cylinder1 = Part.makeCylinder(3, 10, App.Vector(0, 0, 0), App.Vector(1, 0, 0))
cylinder2 = Part.makeCylinder(3, 10, App.Vector(5, 0, -5), App.Vector(0, 0, 1))
fuse = cylinder1.fuse(cylinder2)
Section
Une "section" est l'intersection entre une forme solide et une forme plane. Elle renvoie une courbe d'intersection, une courbe composée d'arêtes.
cylinder1 = Part.makeCylinder(3, 10, App.Vector(0, 0, 0), App.Vector(1, 0, 0))
cylinder2 = Part.makeCylinder(3, 10, App.Vector(5, 0, -5), App.Vector(0, 0, 1))
section = cylinder1.section(cylinder2)
section.Wires
> []
section.Edges
> [<Edge object at 0D87CFE8>, <Edge object at 019564F8>, <Edge object at 0D998458>,
<Edge object at 0D86DE18>, <Edge object at 0D9B8E80>, <Edge object at 012A3640>,
<Edge object at 0D8F4BB0>]
Extrusion
L'extrusion est une action de "pousser" une forme plane dans une certaine direction et résultant en un corps solide. Pensez à un cercle devenant un tube en le "poussant" :
circle = Part.makeCircle(10)
tube = circle.extrude(App.Vector(0, 0, 2))
Si votre cercle est vide, vous obtiendrez un tube vide. Si votre cercle est un disque avec une face pleine, vous obtiendrez un cylindre solide :
wire = Part.Wire(circle)
disc = Part.Face(wire)
cylinder = disc.extrude(App.Vector(0, 0, 2))
Exploration de formes
Vous pouvez facilement explorer la structure de ses données topologique :
import Part
b = Part.makeBox(100, 100, 100)
b.Wires
w = b.Wires[0]
w
w.Wires
w.Vertexes
Part.show(w)
w.Edges
e = w.Edges[0]
e.Vertexes
v = e.Vertexes[0]
v.Point
En tapant les lignes ci-dessus dans l'interpréteur Python, vous gagnerez une bonne compréhension de la structure des objets Part. Ici, notre commande makeBox () créé une forme solide. Ce solide, comme tous les solides de pièce, contient des faces. Les faces contiennent toujours des fils, qui sont des listes d'arêtes qui bordent la face. Chaque face a au moins un fil fermé (il peut en avoir plus si la face a un trou). Dans le fil, nous pouvons regarder chaque bord séparément et à l'intérieur de chaque bord, nous pouvons voir les sommets. Les arêtes droites n'ont que deux sommets, évidemment.
Analyse des arêtes (Edge)
Dans le cas d'un bord (ou arête), qui est une courbe arbitraire, il est fort probable que vous voulez faire une discrétisation. Dans FreeCAD, les bords sont paramétrés par leurs longueurs. Cela signifie, que vous pouvez suivre une arête/courbe par sa longueur :
import Part
box = Part.makeBox(100, 100, 100)
anEdge = box.Edges[0]
print(anEdge.Length)
Maintenant, vous pouvez accéder à un grand nombre de propriétés de l'arête en utilisant sa longueur comme une position. C'est à dire que, si l'arête (ou bord) a une longueur de 100 mm la position de départ est 0 et sa position extrême est 100.
anEdge.tangentAt(0.0) # tangent direction at the beginning
anEdge.valueAt(0.0) # Point at the beginning
anEdge.valueAt(100.0) # Point at the end of the edge
anEdge.derivative1At(50.0) # first derivative of the curve in the middle
anEdge.derivative2At(50.0) # second derivative of the curve in the middle
anEdge.derivative3At(50.0) # third derivative of the curve in the middle
anEdge.centerOfCurvatureAt(50) # center of the curvature for that position
anEdge.curvatureAt(50.0) # the curvature
anEdge.normalAt(50) # normal vector at that position (if defined)
Utilisation de la sélection
Ici, nous allons voir comment nous pouvons utiliser la fonction de sélection, quand l'utilisateur a fait une sélection dans la visionneuse. Tout d'abord, nous créons une boîte (box) et nous l'affichons dans la fenêtre de vue.
import Part
Part.show(Part.makeBox(100, 100, 100))
Gui.SendMsgToActiveView("ViewFit")
Sélectionnez maintenant des faces ou arêtes. Avec ce script, vous pouvez parcourir tous les objets sélectionnés et visionner leurs sous-éléments :
for o in Gui.Selection.getSelectionEx():
print(o.ObjectName)
for s in o.SubElementNames:
print("name: ", s)
for s in o.SubObjects:
print("object: ", s)
Sélectionnez quelques bords et ce script va calculer la longueur :
length = 0.0
for o in Gui.Selection.getSelectionEx():
for s in o.SubObjects:
length += s.Length
print("Length of the selected edges: ", length)
Exemple : la bouteille OCC
Un exemple typique trouvé sur le site Web OpenCasCade Technology est de savoir comment construire une bouteille. C'est aussi un bon exercice pour FreeCAD. En fait, si vous suivez notre exemple ci-dessous et la page OCC simultanément, vous verrez à quel point les structures OCC sont bien implémentées dans FreeCAD. Le script est inclus dans l'installation de FreeCAD (dans le dossier Mod/Part) et peut être appelé à partir de l'interpréteur Python en tapant :
import Part
import MakeBottle
bottle = MakeBottle.makeBottle()
Part.show(bottle)
Le script
Pour les besoins de ce tutoriel, nous considérerons une version réduite du script. Dans cette version, le flacon ne sera pas évidé et le goulot du flacon ne sera pas fileté.
import FreeCAD as App
import Part, math
def makeBottleTut(myWidth = 50.0, myHeight = 70.0, myThickness = 30.0):
aPnt1=App.Vector(-myWidth / 2., 0, 0)
aPnt2=App.Vector(-myWidth / 2., -myThickness / 4., 0)
aPnt3=App.Vector(0, -myThickness / 2., 0)
aPnt4=App.Vector(myWidth / 2., -myThickness / 4., 0)
aPnt5=App.Vector(myWidth / 2., 0, 0)
aArcOfCircle = Part.Arc(aPnt2, aPnt3, aPnt4)
aSegment1=Part.LineSegment(aPnt1, aPnt2)
aSegment2=Part.LineSegment(aPnt4, aPnt5)
aEdge1=aSegment1.toShape()
aEdge2=aArcOfCircle.toShape()
aEdge3=aSegment2.toShape()
aWire=Part.Wire([aEdge1, aEdge2, aEdge3])
aTrsf=App.Matrix()
aTrsf.rotateZ(math.pi) # rotate around the z-axis
aMirroredWire=aWire.copy()
aMirroredWire.transformShape(aTrsf)
myWireProfile=Part.Wire([aWire, aMirroredWire])
myFaceProfile=Part.Face(myWireProfile)
aPrismVec=App.Vector(0, 0, myHeight)
myBody=myFaceProfile.extrude(aPrismVec)
myBody=myBody.makeFillet(myThickness / 12.0, myBody.Edges)
neckLocation=App.Vector(0, 0, myHeight)
neckNormal=App.Vector(0, 0, 1)
myNeckRadius = myThickness / 4.
myNeckHeight = myHeight / 10.
myNeck = Part.makeCylinder(myNeckRadius, myNeckHeight, neckLocation, neckNormal)
myBody = myBody.fuse(myNeck)
return myBody
el = makeBottleTut()
Part.show(el)
Explications détaillées
import FreeCAD as App
import Part, math
Nous aurons, bien sûr, besoin des modules FreeCAD et Part.
def makeBottleTut(myWidth = 50.0, myHeight = 70.0, myThickness = 30.0):
aPnt1=App.Vector(-myWidth / 2., 0, 0)
aPnt2=App.Vector(-myWidth / 2., -myThickness / 4., 0)
aPnt3=App.Vector(0, -myThickness / 2., 0)
aPnt4=App.Vector(myWidth / 2., -myThickness / 4., 0)
aPnt5=App.Vector(myWidth / 2., 0, 0)
Ici, nous définissons notre fonction makeBottleTut. Cette fonction peut être appelée sans argument, comme nous l'avons fait ci-dessus, les valeurs par défaut, de largeur, hauteur et épaisseur seront utilisés. Ensuite, nous définissons une paire de points qui seront utilisés pour la construction de notre profil de base.
...
aArcOfCircle = Part.Arc(aPnt2, aPnt3, aPnt4)
aSegment1=Part.LineSegment(aPnt1, aPnt2)
aSegment2=Part.LineSegment(aPnt4, aPnt5)
Ici, nous définissons la géométrie : un arc, composé de trois points et deux segments de ligne, composés de deux points.
...
aEdge1=aSegment1.toShape()
aEdge2=aArcOfCircle.toShape()
aEdge3=aSegment2.toShape()
aWire=Part.Wire([aEdge1, aEdge2, aEdge3])
Vous vous souvenez de la différence entre la géométrie et les formes ? Nous allons construire les formes de notre forme géométrique. Trois bords (bords ou arêtes peuvent être des segments de droites ou des courbes) puis nous raccordons tous les sommets.
...
aTrsf=App.Matrix()
aTrsf.rotateZ(math.pi) # rotate around the z-axis
aMirroredWire=aWire.copy()
aMirroredWire.transformShape(aTrsf)
myWireProfile=Part.Wire([aWire, aMirroredWire])
Jusqu'à présent, nous n'avons construit qu'un demi-profil. Au lieu de construire tout le profil de la même manière, nous pouvons simplement refléter ce que nous avons fait et coller les deux moitiés ensemble. Nous créons d'abord une matrice. Une matrice est un moyen très courant d'appliquer des transformations aux objets du monde 3D, car il peut contenir dans une seule structure tous les les transformations que les objets 3D peuvent subir (déplacement, rotation et échelle). Après avoir créé la matrice, nous la reflétons, puis nous créons une copie de notre fil et lui appliquer la matrice de transformation. Nous avons maintenant deux fils, et nous pouvons en faire un troisième fil, car les fils sont en fait des listes d'arêtes.
...
myFaceProfile=Part.Face(myWireProfile)
aPrismVec=App.Vector(0, 0, myHeight)
myBody=myFaceProfile.extrude(aPrismVec)
myBody=myBody.makeFillet(myThickness / 12.0, myBody.Edges)
Maintenant, nous avons un contour fermé, il peut être transformé en une face. Une fois que nous avons une face, nous pouvons l'extruder. Une fois fait, nous avons un solide. Puis, nous appliquons un filet à notre objet car nous voulons lui donner un aspect "design", n'est-ce pas ?
...
neckLocation=App.Vector(0, 0, myHeight)
neckNormal=App.Vector(0, 0, 1)
myNeckRadius = myThickness / 4.
myNeckHeight = myHeight / 10.
myNeck = Part.makeCylinder(myNeckRadius, myNeckHeight, neckLocation, neckNormal)
À ce stade, le corps de notre bouteille est fabriqué mais nous devons encore créer un goulot. On fait un nouveau solide avec un cylindre.
...
myBody = myBody.fuse(myNeck)
L'opération de fusion est très puissante. Elle se charge de coller ce qui doit l'être et de retirer les pièces qui doivent l'être.
...
return myBody
Puis, nous revenons à notre bouteille (Part solid), qui est le résultat de notre fonction.
el = makeBottleTut()
Part.show(el)
Enfin, nous appelons la fonction pour créer la pièce puis la rendons visible.
Exemple : cube percé
Ici un exemple complet de construction d'un cube percé.
La construction se fait face par face. Quand le cube est terminé, il est évidé d'un cylindre traversant.
import FreeCAD as App
import Part, math
size = 10
poly = Part.makePolygon([(0, 0, 0), (size, 0, 0), (size, 0, size), (0, 0, size), (0, 0, 0)])
face1 = Part.Face(poly)
face2 = Part.Face(poly)
face3 = Part.Face(poly)
face4 = Part.Face(poly)
face5 = Part.Face(poly)
face6 = Part.Face(poly)
myMat = App.Matrix()
myMat.rotateZ(math.pi / 2)
face2.transformShape(myMat)
face2.translate(App.Vector(size, 0, 0))
myMat.rotateZ(math.pi / 2)
face3.transformShape(myMat)
face3.translate(App.Vector(size, size, 0))
myMat.rotateZ(math.pi / 2)
face4.transformShape(myMat)
face4.translate(App.Vector(0, size, 0))
myMat = App.Matrix()
myMat.rotateX(-math.pi / 2)
face5.transformShape(myMat)
face6.transformShape(myMat)
face6.translate(App.Vector(0, 0, size))
myShell = Part.makeShell([face1, face2, face3, face4, face5, face6])
mySolid = Part.makeSolid(myShell)
myCyl = Part.makeCylinder(2, 20)
myCyl.translate(App.Vector(size / 2, size / 2, 0))
cut_part = mySolid.cut(myCyl)
Part.show(cut_part)
Chargement et sauvegarde
Il existe plusieurs façons de sauvegarder votre travail. Vous pouvez bien sûr enregistrer votre document FreeCAD, mais vous pouvez également enregistrer des objets Part directement dans des formats CAO courants, tels que BREP, IGS, STEP et STL.
L'enregistrement d'une forme (un projet) dans un fichier est facile, il y a les fonctions exportBrep(), exportIges(), exportStep() et exportStl() qui sont des méthodes disponibles pour toutes les formes d'objets. Donc, en faisant :
import Part
s = Part.makeBox(10, 10, 10)
s.exportStep("test.stp")
enregistrera notre boîte dans un fichier STEP. Pour charger un fichier BREP, IGES ou STEP :
import Part
s = Part.Shape()
s.read("test.stp")
Pour convertir un fichier STEP en fichier IGS :
import Part
s = Part.Shape()
s.read("file.stp") # incoming file igs, stp, stl, brep
s.exportIges("file.igs") # outbound file igs
- Scripts FreeCAD : Python, Introduction à Python, Tutoriel sur les scripts Python, Débuter avec les scripts
- Modules : Modules intégrés, Unités, Quantity
- Ateliers : Création d'atelier, Commands Gui, Les commandes, Installer des ateliers supplémentaires
- Maillages et objets Parts : Scripts Mesh, Script de données topologiques, Conversion objet Mesh en Part, PythonOCC
- Objets paramétriques : Objets créés par script, Viewproviders (Icône personnalisée dans l'arborescence)
- Scénographie : Graphe de scène Coin (Inventor), Pivy
- Interface graphique : Création d'interface, Création d'une boite de dialogue (1, 2, 3, 4, 5), PySide, Exemples PySide débutant, intermédiaire, expérimenté
- Macros : Macros, Comment installer des macros
- Intégration : Intégrer FreeCAD, Intégration de FreeCADGui
- Autre : Expressions, Extraits de codes, Fonction - tracer une ligne, Bibliothèque mathématique vectorielle de FreeCAD (déprécié)