Topological data scripting/ro

Other languages:

Scripted objects

Introducere

Aici vă vom explica cum să controlați Part Workbench direct de la interpretorul FreeCAD Python sau de la orice script extern. Elementele de bază despre programarea script datelor topologice sunt descrise în Part Module Explaining the concepts. fiți siguri că a-ți răsfoit secțiunea Scripting și paginile FreeCAD Scripting Basics dacă aveți nevoie de mai multe informații despre cum funcționaează programarea python in FreeCAD.

Here we will explain to you how to control the Part module directly from the FreeCAD Python interpreter, or from any external script. Be sure to browse the Scripting section and the FreeCAD Scripting Basics pages if you need more information about how Python scripting works in FreeCAD. If you are new to Python, it is a good idea to first read the Introduction to Python.

See also

Class Diagram

Aceasta Unified Modeling Language (UML) o trecere în revistă a celor mai importante clase a modului Piese:

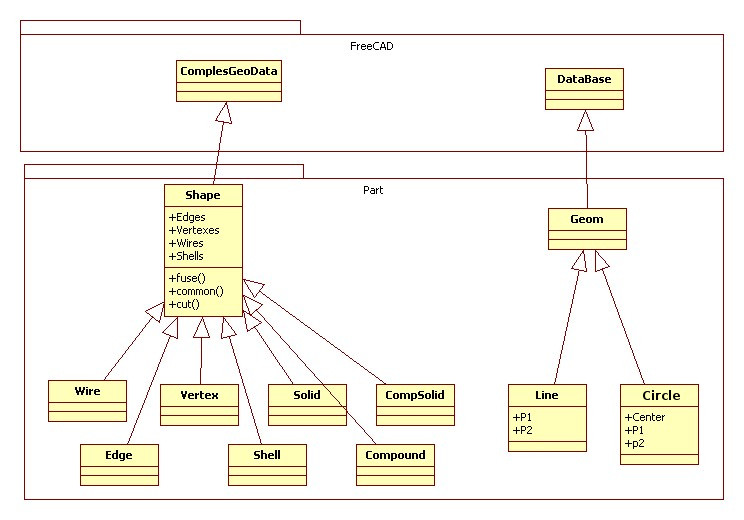
Python classes of the Part module

This is a Unified Modeling Language (UML) overview of the most important classes of the Part module:

Geometrie

Obiectele geometrice reprezintă blocul de construcție al tuturor obiectelor topologice:

Geom Clasă de bază a obiectelor geometrice
Line o linie dreaptă în 3D, definită de punctul de plecare și de cel de sosire
Circle Cerc sau arc de cerc definit prin centru și punctele de start și de finiș
...... Și în curând mai multe

The geometric objects are the building blocks of all topological objects:

Geom Base class of the geometric objects.
Line A straight line in 3D, defined by starting point and end point.
Circle Circle or circle segment defined by a center point and start and end point.
Etc.

Topologie

Următoarele date topologice sunt disponibile:

Compound Un grup al oricărui tip de obiect topologic.
Compsolid Un solid compozit este un set de solide conectate prin fațetele lor. Extinde noțiunile de WIRE și SHELL la solide.
Solid O partea a spațiului limitată de cochilii. Are trei dimensiuni
Shell Un set da fațete conectate prin muchiile lor. O cochilie poate fi deschisă sau închisă.
Face In 2D este o parte a unui plan; in 3D este o parte a unei suprafețe.

Geometria sa este constrânsă(tăiată) de contururi. Este bidimensională.

Wire Un set de margini conectate prin vârfurile lor. Poate fi un contur deschis sau închis, în funcție de faptul dacă marginile sunt legate sau nu.
Edge Un element topologic corespunzător unei curbe reținute. O margine este în general limitată de vârfuri. Este unidimensională.
Vertex Un element topologic corespunzător unui punct. Are dimensiune zero.
Shape Un termen generic care acoperă toate cele de mai sus.

The following topological data types are available:

Compound A group of any type of topological objects.
Compsolid A composite solid is a set of solids connected by their faces. It expands the notions of WIRE and SHELL to solids.
Solid A part of space limited by shells. It is three dimensional.
Shell A set of faces connected by their edges. A shell can be open or closed.
Face In 2D it is part of a plane; in 3D it is part of a surface. Its geometry is constrained (trimmed) by contours. It is two dimensional.
Wire A set of edges connected by their vertices. It can be an open or closed contour depending on whether the edges are linked or not.
Edge A topological element corresponding to a restrained curve. An edge is generally limited by vertices. It has one dimension.
Vertex A topological element corresponding to a point. It has zero dimension.
Shape A generic term covering all of the above.

Exemplul rapid: crearea unei topologii simple

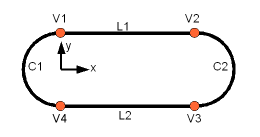
Acum vom crea o topologie construind-o din geometrie mai simplă. Ca studiu de caz, folosim o parte din imaginea din care face parte patru vârfuri, două cercuri și două linii.

Crearea Geometriei

Mai întâi trebuie să creăm părțile geometrice distincte ale acestui fir. Și trebuie să avem grijă de vârfurile părților geometrice se se afle în aceeași poziție. Altfel, mai târziu, s-ar putea să nu fim capabil să conectăm părțile geometrice la o topologie!

First we create the distinct geometric parts of this wire. Making sure that parts that have to be connected later share the same vertices.

Așa creăm primul dintre puncte:

import FreeCAD as App
import Part
V1 = App.Vector(0, 10, 0)
V2 = App.Vector(30, 10, 0)
V3 = App.Vector(30, -10, 0)
V4 = App.Vector(0, -10, 0)

Arc

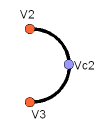
Pentru a crea un arc de cerc vom face un punct ca reper și vom crea arcul de cerc prin trei puncte:

VC1 = App.Vector(-10, 0, 0)
C1 = Part.Arc(V1, VC1, V4)
VC2 = App.Vector(40, 0, 0)
C2 = Part.Arc(V2, VC2, V3)

Linie

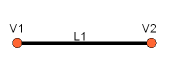
Segmentul de linie poate fi creat foarte simplu din punctele:

L1 = Part.LineSegment(V1, V2)
L2 = Part.LineSegment(V3, V4)

Punem totul laolaltă

Ultimul pas este de a conecta elementele geometrice de bază împreună într-o forma topologică:

The last step is to put the geometric base elements together and bake a topological shape:

S1 = Part.Shape([C1, L1, C2, L2])

Facem o prismă

Acum extrudem firul într-o direcție și facem o formă 3D :

Now extrude the wire in a direction and make an actual 3D shape:

W = Part.Wire(S1.Edges)
P = W.extrude(App.Vector(0, 0, 10))

Afișăm totul

Part.show(P)

Crearea formelor de bază

Puteți crea cu ușurință obiecte topologice de bază cu ajutorul funcției "Make ... ()" metode de la modulul Part:

You can easily create basic topological objects with the make...() methods from the Part module:

b = Part.makeBox(100, 100, 100)
Part.show(b)

Câteva metode disponibile de make...() :

makeBox(l,w,h): Construirea unui paralelipiped localizat în punctul p orientat în direcția d având dimensiunile (l,w,h)
makeCircle(radius): Construirea cercului cu o rază dată
makeCone(radius1,radius2,height): Construirea unui con cu (raza1,raza2,înălțime)
makeCylinder(radius,height): Construirea unui cilindru cunoscând raza și înălțimea.
makeLine((x1,y1,z1),(x2,y2,z2)): Construirea unei linii între 2 puncte
makePlane(length,width): construirea unui plan cunoscând lungimea și lățimea
makePolygon(list): construirea unui poligon având o listă de puncte
makeSphere(radius): Construirea unei sfere de rază dată
makeTorus(radius1,radius2): construirea unui torus cuoscând raza 1 și raza 2

Vezi pagina Part API pentru o listă completa a metodelor disponibile în modulul Part.

Importare modulelor necesare

Mai întâi trebuie să importăm modulul Part astfel încât să putem folosi conținutul său în Python. De asemenea, vom importa modulul Base din interiorul modulului FreeCAD:

First we need to import the FreeCAD and Part modules so we can use their contents in Python:

import FreeCAD as App
import Part

Crearea unui Vector

Vectorssunt una dintre cele mai importante piese de informații când construim forme geometrice. Acestea conțin 3 numere de obicei (dar nu este obligatoriu întotdeauna) coordonatele carteziene x, y și z. Creați un vector ca acesta:

Vectors are one of the most important pieces of information when building shapes. They usually contain three numbers (but not necessarily always): the X, Y and Z cartesian coordinates. You create a vector like this:

myVector = App.Vector(3, 2, 0)

Tocmai am creat un vector la coordonatele x = 3, y = 2, z = 0. În modulul Part, vectorii sunt folosiți peste tot. Formele de Piese utilizează de asemenea un alt tip de punct reprezentare, numită Vertex, care nu este nimic altceva decât un container pentru un vector. Accesați vectorul unui vârf ca acesta:

myVertex = myShape.Vertexes[0]
print(myVertex.Point)
> Vector (3, 2, 0)

Crearea unei muchii

O margine nu este altceva decât o linie cu două vârfuri:

An edge is nothing but a line with two vertices:

edge = Part.makeLine((0, 0, 0), (10, 0, 0))
edge.Vertexes
> [<Vertex object at 01877430>, <Vertex object at 014888E0>]

Notă: De asemenea, puteți crea o margine definită de doi vectori:

vec1 = App.Vector(0, 0, 0)
vec2 = App.Vector(10, 0, 0)
line = Part.LineSegment(vec1, vec2)
edge = line.toShape()

Puteți găsi lungimea și centrul unei muchii astfel:

edge.Length
> 10.0
edge.CenterOfMass
> Vector (5, 0, 0)

Afișarea formei pe ecran

Până acum, am creat un obiect de margine, dar nu apare nicăieri pe ecran. Acest lucru se datorează faptului că doar am manipulat obiectele de tip python aici. Scena 3D FreeCAD afișează doar ceea ce îi spui să afișeze. Pentru a face acest lucru, folosim acest lucru simplu Pentru a realiza asta, utilizăm această metodă simplă:

So far we created an edge object, but it doesn't appear anywhere on the screen. This is because the FreeCAD 3D scene only displays what you tell it to display. To do that, we use this simple method:

Part.show(edge)

Un obiect va fi creat în documentul nostru FreeCAD, și forma noastră "muchie" va fi atribuită. Utilizați acest lucru când este timpul să vă afișați creație pe ecran.

Crearea unui fir/contur/polilinie

Un fir este o linie multi-margine și poate fi creat dintr-o listă de margini sau chiar o listă de fire:

A wire is a multi-edge line and can be created from a list of edges or even a list of wires:

edge1 = Part.makeLine((0, 0, 0), (10, 0, 0))
edge2 = Part.makeLine((10, 0, 0), (10, 10, 0))
wire1 = Part.Wire([edge1, edge2]) 
edge3 = Part.makeLine((10, 10, 0), (0, 10, 0))
edge4 = Part.makeLine((0, 10, 0), (0, 0, 0))
wire2 = Part.Wire([edge3, edge4])
wire3 = Part.Wire([wire1, wire2])
wire3.Edges
> [<Edge object at 016695F8>, <Edge object at 0197AED8>, <Edge object at 01828B20>, <Edge object at 0190A788>]
Part.show(wire3)

Part.show(wire3) va afișa cele 4 margini care compun firul/polilinia noastră. alte informațiile utile pot fi ușor recuperate:

wire3.Length
> 40.0
wire3.CenterOfMass
> Vector (5, 5, 0)
wire3.isClosed()
> True
wire2.isClosed()
> False

Crearea unei Fațete

Doar fațetele create de firele/poliliniile închise vor fi valide. În acest exemplu, wire3 este un contur închis dar wire2 nu este un contur închis(vezi mai sus)

Only faces created from closed wires will be valid. In this example, wire3 is a closed wire but wire2 is not (see above):

face = Part.Face(wire3)
face.Area
> 99.99999999999999
face.CenterOfMass
> Vector (5, 5, 0)
face.Length
> 40.0
face.isValid()
> True
sface = Part.Face(wire2)
sface.isValid()
> False

Numai fațetele vor avea o arie, poliliniile și muchiile nu posedă așa ceva.

Crearea unui Cerc

Un cerc poate fi creat pur și simplu astfel:

A circle can be created like this:

circle = Part.makeCircle(10)
circle.Curve
> Circle (Radius : 10, Position : (0, 0, 0), Direction : (0, 0, 1))

Dacă vreți să îl creați la o anumită poziție și într-o anumită direcție:

ccircle = Part.makeCircle(10, App.Vector(10, 0, 0), App.Vector(1, 0, 0))
ccircle.Curve
> Circle (Radius : 10, Position : (10, 0, 0), Direction : (1, 0, 0))

cercul va fi creat la distanța 10 unități de la axa x și va fi orientat spre axa x. Notă: makeCircle acceptă numai Base.Vector () pentru poziție și normal, dar nu tuple. Puteți, de asemenea, să creați o parte a cercului dând unghiul de pornire și unghiul de capăt ca de exemplu:

from math import pi
arc1 = Part.makeCircle(10, App.Vector(0, 0, 0), App.Vector(0, 0, 1), 0, 180)
arc2 = Part.makeCircle(10, App.Vector(0, 0, 0), App.Vector(0, 0, 1), 180, 360)

Ambele atât arc1 cât și arc2 vor face un cerc. Trebuie introduse unghiuri în grade, dacă aveți radiani pur și simplu le convertiți folosind formula: grade = radiani * 180 / PI sau folosind modulul matematic al lui python (după importul efectuat matematica, desigur):

import math
degrees = math.degrees(radians)

Crearea unui Arc de-a lungul punctelor

Din păcate, nu există nicio funcție makeArc, dar avem funcția Part.Arc pentru a crea un arc de-a lungul a trei puncte. Practic, putem să ne imaginăm un arc de cerc atașat la un punct de plecare, trecând printr-un punct central și terminându-se într-un punct final. Part.Arc creează un obiect arc pe care .toShape() trebuie apelat pentru a obține un obiect muchie, în același mod ca atunci când utilizați Part.LineSegment în loc de Part.makeLine.

Unfortunately there is no makeArc() function, but we have the Part.Arc() function to create an arc through three points. It creates an arc object joining the start point to the end point through the middle point. The arc object's toShape() function must be called to get an edge object, the same as when using Part.LineSegment instead of Part.makeLine.

arc = Part.Arc(App.Vector(0, 0, 0), App.Vector(0, 5, 0), App.Vector(5, 5, 0))
arc
> <Arc object>
arc_edge = arc.toShape()
Part.show(arc_edge)

Arc only accepts Base.Vector() for points but not tuples. arc_edge is what we want which we can display using Part.show(arc_edge). You can also obtain an arc by using a portion of a circle:

from math import pi
circle = Part.Circle(App.Vector(0, 0, 0), App.Vector(0, 0, 1), 10)
arc = Part.Arc(circle,0,pi)

Arcurile sunt muchii valide, ca liniile. Deci, ele pot fi folosite și în polilinii/contururi/fire.

Crearea unui poligon

Un poligon este o polilinie simplă cu multiple segemente de linii drepte. funcția makePolygon ia o listă de puncte și creează o polilinie de-a lungul acestor puncte:

A polygon is simply a wire with multiple straight edges. The makePolygon() function takes a list of points and creates a wire through those points:

lshape_wire = Part.makePolygon([App.Vector(0, 5, 0), App.Vector(0, 0, 0), App.Vector(5, 0, 0)])

Crearea unei curbe Bezier

Curbele Bézier sunt folosite pentru a modela curbele netede folosind o serie de repere (puncte de control) și cu un numar mare de reprezentari la precizie (fluiditatea curbei). Funcția de mai jos face Part.BezierCurve dintr-o serie de puncte FreeCAD.Vector. (Notă: indicele primului reper începe de la 1, și nu de la 0.)

Bézier curves are used to model smooth curves using a series of poles (points) and optional weights. The function below makes a Part.BezierCurve() from a series of FreeCAD.Vector() points. Note: when "getting" and "setting" a single pole or weight, indices start at 1, not 0.

def makeBCurveEdge(Points):
   geomCurve = Part.BezierCurve()
   geomCurve.setPoles(Points)
   edge = Part.Edge(geomCurve)
   return(edge)

Crearea unui Plan

A Plane este o suprafață simplă rectangulară. Meteoda pentru crearea unuia este aceasta: makePlane(length,width,[start_pnt,dir_normal]). Implicit start_pnt = Vector(0,0,0) and dir_normal = Vector(0,0,1). Utilizând dir_normal = Vector(0,0,1) va crea un plan pe axa z, în timp ce dir_normal = Vector(1,0,0) va crea planul pe axa x:

A Plane is a flat rectangular surface. The method used to create one is makePlane(length, width, [start_pnt, dir_normal]). By default start_pnt = Vector(0, 0, 0) and dir_normal = Vector(0, 0, 1). Using dir_normal = Vector(0, 0, 1) will create the plane facing in the positive Z axis direction, while dir_normal = Vector(1, 0, 0) will create the plane facing in the positive X axis direction:

plane = Part.makePlane(2, 2)
plane
> <Face object at 028AF990>
plane = Part.makePlane(2, 2, App.Vector(3, 0, 0), App.Vector(0, 1, 0))
plane.BoundBox
> BoundBox (3, 0, 0, 5, 0, 2)

BoundBox este un cuboid care înconjoară planul cu o diagonală începând de la (3.0.0) și se termină la (5.0.2). Aici grosimea BoundBox în axa y este zero, deoarece forma noastră este complet plană.

Notă: makePlane acceptă doar Base.Vector() pentru start_pnt and dir_normal dar nu și tuplele

Crearea unei elipse

Pentru a crea o elipsă sunt mai multe căi:

There are several ways to create an ellipse:

Part.Ellipse()

Crează o elipsă cu raza mare 2 și cu raza mică 1 cu centrul în (0,0,0)

Part.Ellipse(Ellipse)

Creațo p copie a elipsei date

Part.Ellipse(S1, S2, Center)

Creează o elipsă centrat pe punctul central, unde planul elipsa este definită de Centrul, S1 și S2, axa sa principală este definită de Centru și S1, semiaxa sa majoră este distanța dintre centrul și S1, iar semiaxa sa minoră este distanța dintre S2 și axa principală.

Part.Ellipse(Center, MajorRadius, MinorRadius)

Creează o elipsă cu semiaxa majoră și cu o semiaxă minoră MajorRadius and MinorRadius, și localizată în planul definit de către Center și normala (0,0,1)

eli = Part.Ellipse(App.Vector(10, 0, 0), App.Vector(0, 5, 0), App.Vector(0, 0, 0))
Part.show(eli.toShape())

În codul de mai sus am trecut S1, S2 și centrul. În mod similar cu Arc, Ellipse creează, de asemenea, un obiect de elipsă, dar nu margine, așa că trebuie să convertiți-l în margine folosind toShape () pentru afișare.

Notă: Doar Arc aceptă Base.Vector() pentru puncte dar nu pentru tuple

eli = Part.Ellipse(App.Vector(0, 0, 0), 10, 5)
Part.show(eli.toShape())

pentru constructorul Ellipse de mai sus am trecut centrul, MajorRadius and MinorRadius

Crearea unui Tor

Folosind metoda makeTorus(radius1,radius2,[pnt,dir,angle1,angle2,angle]). Implicit avem pnt=Vector(0,0,0),dir=Vector(0,0,1),angle1=0,angle2=360 and angle=360. Considerați un tor ca pe un mic cerca care baliază de-a lungul unu cerc mare. Radius1 este raza cercului mare , iar radius2 este raza cercului mic, pnt este centrul torului și dir este direcția normalei. angle1 and angle2 sunt unghiurile în radiani pentru cercul mic, ultimul parametru -unghiul este pentru a face o secțiune în tor:

Using makeTorus(radius1, radius2, [pnt, dir, angle1, angle2, angle]). By default pnt = Vector(0, 0, 0), dir = Vector(0, 0, 1), angle1 = 0, angle2 = 360 and angle = 360. Consider a torus as small circle sweeping along a big circle. Radius1 is the radius of the big circle, radius2 is the radius of the small circle, pnt is the center of the torus and dir is the normal direction. angle1 and angle2 are angles in degrees for the small circle; the last angle parameter is to make a section of the torus:

torus = Part.makeTorus(10, 2)

Codul de deasupra va crea un tor cu diametrul 20(raza 10) și grosimea 4 (raza cercului mic 2)

tor=Part.makeTorus(10, 5, App.Vector(0, 0, 0), App.Vector(0, 0, 1), 0, 180)

codul de mai sus va crea o felie de tor

tor=Part.makeTorus(10, 5, App.Vector(0, 0, 0), App.Vector(0, 0, 1), 0, 360, 180)

Codul de mai sus va crea un semtor, numai ultimul parametru este schimbat adică unghiul și unghiurile rămase sunt implicite. Dând unghiul 180 va a crea tor de la 0 la 180, adică un jumătate de tor.

Crearea unui paralelipiped sau cuboid

Utilizând makeBox(length,width,height,[pnt,dir]). Implicit pnt=Vector(0,0,0) and dir=Vector(0,0,1)

Using makeBox(length, width, height, [pnt, dir]). By default pnt = Vector(0, 0, 0) and dir = Vector(0, 0, 1).

box = Part.makeBox(10, 10, 10)
len(box.Vertexes)
> 8

Crearea unei sfere

Utilizând makeSphere(radius,[pnt, dir, angle1,angle2,angle3]). Implicit avem pnt=Vector(0,0,0), dir=Vector(0,0,1), angle1=-90, angle2=90 and angle3=360. angle1 și angle2 sunt verticala minimă și verticala maximă ale sferei, angle3 diametrul sferei.

Using makeSphere(radius, [pnt, dir, angle1, angle2, angle3]). By default pnt = Vector(0, 0, 0), dir = Vector(0, 0, 1), angle1 = -90, angle2 = 90 and angle3 = 360. Angle1 and angle2 are the vertical minimum and maximum of the sphere, angle3 is the sphere diameter.

sphere = Part.makeSphere(10)
hemisphere = Part.makeSphere(10, App.Vector(0, 0, 0), App.Vector(0, 0, 1), -90, 90, 180)

Crearea unui cilindru

Utilizând makeCylinder(radius,height,[pnt,dir,angle]). Implicat avem pnt=Vector(0,0,0),dir=Vector(0,0,1) și angle=360

Using makeCylinder(radius, height, [pnt, dir, angle]). By default pnt = Vector(0, 0, 0), dir = Vector(0, 0, 1) and angle = 360.

cylinder = Part.makeCylinder(5, 20)
partCylinder = Part.makeCylinder(5, 20, App.Vector(20, 0, 0), App.Vector(0, 0, 1), 180)

Crearea unui Con

Utilizând makeCone(radius1,radius2,height,[pnt,dir,angle]). Implicit avem pnt=Vector(0,0,0), dir=Vector(0,0,1) and angle=360

Using makeCone(radius1, radius2, height, [pnt, dir, angle]). By default pnt = Vector(0, 0, 0), dir = Vector(0, 0, 1) and angle = 360.

cone = Part.makeCone(10, 0, 20)
semicone = Part.makeCone(10, 0, 20, App.Vector(20, 0, 0), App.Vector(0, 0, 1), 180)

Modificarea Formelor geometrice

Sunt mai multe moduri de a modifica forme. Unele sunt operații simple de transformare cum ar fi mișcările sau formele rotative, altele sunt mai complexe, cum ar fi unirea și scăderea unei forme de alta. Țineți cont de asta

There are several ways to modify shapes. Some are simple transformation operations such as moving or rotating shapes, others are more complex, such as unioning and subtracting one shape from another.

Operații de Transformare

Translatarea unei forme

Translatarea estr de fapt actul de mutarea a unei forme dintr-un loc în altul. Orice formă (muchie, fațetă, cube, etc...) poate fi translată în același mod:

Translating is the act of moving a shape from one place to another. Any shape (edge, face, cube, etc...) can be translated the same way:

myShape = Part.makeBox(2, 2, 2)
myShape.translate(App.Vector(2, 0, 0))

Aceasta va muta forma noastră "myShape" 2 unități in direcția x .

Rotația unei forme

Pentru a roti o formă, aveți nevoie de uncentru de rotație, axa, și unghiul de rotație:

To rotate a shape, you need to specify the rotation center, the axis, and the rotation angle:

myShape.rotate(App.Vector(0, 0, 0),App.Vector(0, 0, 1), 180)

Codul de mai sus va roti forma cu 180 degrees în jurul axei Z .

Transformările generice cu matrici

O matrice este o modalitate foarte convenabilă de a stoca transformările în lumea reală 3D. Într-o singură matrice, puteți defini valorile de translația, rotirea și scalarea care trebuie aplicate unui obiect. De exemplu:

A matrix is a very convenient way to store transformations in the 3D world. In a single matrix, you can set translation, rotation and scaling values to be applied to an object. For example:

myMat = App.Matrix()
myMat.move(App.Vector(2, 0, 0))
myMat.rotateZ(math.pi/2)

Notă: Matricile FreeCAD lucrează în radiani. De altfel, aproape toate operațiile de matrice care iau un vector pot lua de asemenea 3 numere, astfel încât cele două linii fac același lucru:

myMat.move(2, 0, 0)
myMat.move(App.Vector(2, 0, 0))

Atunci când matricea noastră este definită, o putem aplica formei noastre. FreeCAD oferă 2 metode pentru a face acest lucru: transformShape() and transformGeometry(). Diferența este că, cu prima, sunteți siguri că nu vor avea loc deformări (a se vedea "scalarea unei forme" de mai jos). Deci, putem aplica transformarea noastră astfel:

myShape.transformShape(myMat)

ori

myShape.transformGeometry(myMat)

Scalarea unei forme geometrice

Scalarea unei forme este o operațiune mai periculoasă deoarece, spre deosebire de translație sau rotație, scalarea neuniformă (cu valori diferite pentru x, y și z) poate modifica structura formei. De exemplu, scalarea unui cerc cu o valoare mai mare pe orizontală decât pe verticală îl va transforma într-o elipsă, care se comportă matematic foarte diferit. Pentru scalare, noi nu putem folosi transformShape, trebuie să folosimtransformGeometry():

Scaling a shape is a more dangerous operation because, unlike translation or rotation, scaling non-uniformly (with different values for X, Y and Z) can modify the structure of the shape. For example, scaling a circle with a higher value horizontally than vertically will transform it into an ellipse, which behaves mathematically very differently. For scaling, we cannot use the transformShape(), we must use transformGeometry():

myMat = App.Matrix()
myMat.scale(2, 1, 1)
myShape=myShape.transformGeometry(myMat)

Operații Booleene

Subtraction

Scăderea unei forme de la alta se numește "tăiat" în jargonul OCC/FreeCAD și se face astfel:

Subtracting a shape from another one is called "cut" in FreeCAD and is done like this:

cylinder = Part.makeCylinder(3, 10, App.Vector(0, 0, 0), App.Vector(1, 0, 0))
sphere = Part.makeSphere(5, App.Vector(5, 0, 0))
diff = cylinder.cut(sphere)

Intersection

În același mod, intersecția dintre două forme este denumită "comună" și se face pe aici:

The same way, the intersection between two shapes is called "common" and is done this way:

cylinder1 = Part.makeCylinder(3, 10, App.Vector(0, 0, 0), App.Vector(1, 0, 0))
cylinder2 = Part.makeCylinder(3, 10, App.Vector(5, 0, -5), App.Vector(0, 0, 1))
common = cylinder1.common(cylinder2)

Union

Unionea este numită "fuse" și lucrează în același mod:

Union is called "fuse" and works the same way:

cylinder1 = Part.makeCylinder(3, 10, App.Vector(0, 0, 0), App.Vector(1, 0, 0))
cylinder2 = Part.makeCylinder(3, 10, App.Vector(5, 0, -5), App.Vector(0, 0, 1))
fuse = cylinder1.fuse(cylinder2)

Section

O secțiune este intersecția dintre o formă solidă și o formă plană. Va returna o curbă de intersecție, un compus cu margini

A "section" is the intersection between a solid shape and a plane shape. It will return an intersection curve, a compound curve composed of edges.

cylinder1 = Part.makeCylinder(3, 10, App.Vector(0, 0, 0), App.Vector(1, 0, 0))
cylinder2 = Part.makeCylinder(3, 10, App.Vector(5, 0, -5), App.Vector(0, 0, 1))
section = cylinder1.section(cylinder2)
section.Wires
> []
section.Edges
> [<Edge object at 0D87CFE8>, <Edge object at 019564F8>, <Edge object at 0D998458>, 
 <Edge  object at 0D86DE18>, <Edge object at 0D9B8E80>, <Edge object at 012A3640>, 
 <Edge object at 0D8F4BB0>]

Extrusion

Extrudarea este actul de "împingere" a unei forme plate într-o anumită direcție care are ca rezultat un corp solid. Gândiți-vă la un cerc devenind un tub prin "împingerea lui":

Extrusion is the act of "pushing" a flat shape in a certain direction, resulting in a solid body. Think of a circle becoming a tube by "pushing it out":

circle = Part.makeCircle(10)
tube = circle.extrude(App.Vector(0, 0, 2))

Dacă cercul dvs. este gol, veți obține un tub gol. Dacă cercul dvs. este de fapt un disc, cu o față plină, veți obține un cilindru solid:

wire = Part.Wire(circle)
disc = Part.Face(wire)
cylinder = disc.extrude(App.Vector(0, 0, 2))

Explorarea formelor

Puteți explora ușor structura datelor topologice:

You can easily explore the topological data structure:

import Part
b = Part.makeBox(100, 100, 100)
b.Wires
w = b.Wires[0]
w
w.Wires
w.Vertexes
Part.show(w)
w.Edges
e = w.Edges[0]
e.Vertexes
v = e.Vertexes[0]
v.Point

Dacă tastați liniile de mai sus în interpretul python, veți câștiga o bună înțelegere a structurii obiectelor Part. Aici, comanda makeBox () a creat o formă solidă. Acest solid, ca toate componentele solide, conține fațete. Fețele conțin întotdeauna polilinii, care sunt liste de margini care delimitează fața. Fiecare față are cel puțin o polilinie închisă (poate avea mai multe dacă fața are una sau mai multe găuri). În polilinie, putem privi la fiecare margine separat, iar în interiorul fiecărei margini, putem vedea vârfurile. Liniile drepte au doar două vârfuri, evident.

Analiza muchiei

În cazul unei muchii, care este o curbă arbitrară, este cel mai probabil să doriți a face o discretizare. În FreeCAD marginile sunt parametrizate după lungimile lor. Asta înseamnă ca puteți parcurge o margine/curba pe lungimea ei:

In case of an edge, which is an arbitrary curve, it's most likely you want to do a discretization. In FreeCAD the edges are parametrized by their lengths. That means you can walk an edge/curve by its length:

import Part
box = Part.makeBox(100, 100, 100)
anEdge = box.Edges[0]
print(anEdge.Length)

Now you can access a lot of properties of the edge by using the length as a position. That means if the edge is 100mm long the start position is 0 and the end position 100.

anEdge.tangentAt(0.0)          # tangent direction at the beginning
anEdge.valueAt(0.0)            # Point at the beginning
anEdge.valueAt(100.0)          # Point at the end of the edge
anEdge.derivative1At(50.0)     # first derivative of the curve in the middle
anEdge.derivative2At(50.0)     # second derivative of the curve in the middle
anEdge.derivative3At(50.0)     # third derivative of the curve in the middle
anEdge.centerOfCurvatureAt(50) # center of the curvature for that position
anEdge.curvatureAt(50.0)       # the curvature
anEdge.normalAt(50)            # normal vector at that position (if defined)

Utilizarea selecție

Aici vedem acum modul în care putem folosi selecția utilizată de utilizator în vizualizator. Mai întâi de toate, creăm o casetă și o afișează în vizualizator

Here we see now how we can use a selection the user did in the viewer. First of all we create a box and show it in the viewer.

import Part
Part.show(Part.makeBox(100, 100, 100))
Gui.SendMsgToActiveView("ViewFit")

Selectați acum unele fețe sau margini. Cu acest script puteți itera toate obiectele selectate și sub-elementele acestora:

for o in Gui.Selection.getSelectionEx():
    print(o.ObjectName)
    for s in o.SubElementNames:
        print("name: ", s)
        for s in o.SubObjects:
            print("object: ", s)

Selectați unele margini și acest progrămel script va calcula lungimea:

length = 0.0
for o in Gui.Selection.getSelectionEx():
    for s in o.SubObjects:
        length += s.Length

print("Length of the selected edges: ", length)

Exemplul complet : Sticla OCC (Open CASCADE Technology)

Un exemplu tipic găsiți în OpenCasCade Technology Tutorial Este cum se construiește o sticlă. Acesta este un exercițiu bun și pentru FreeCAD. De fapt, puteți urma exemplul nostru de mai jos și pagina OCC simultan, veți înțelege cum sunt implementate structurile OCC în FreeCAD. Scenariul complet de mai jos este, de asemenea, inclus în instalarea FreeCAD (în interiorul folderului Mod/Part) și poate fi apelat de la interpretul python prin tastarea:

A typical example found on the OpenCasCade Technology website is how to build a bottle. This is a good exercise for FreeCAD too. In fact, if you follow our example below and the OCC page simultaneously, you will see how well OCC structures are implemented in FreeCAD. The script is included in the FreeCAD installation (inside the Mod/Part folder) and can be called from the Python interpreter by typing:

import Part
import MakeBottle
bottle = MakeBottle.makeBottle()
Part.show(bottle)

Programul script complet

aici este programul script complet MakeBottle:

For the purpose of this tutorial we will consider a reduced version of the script. In this version the bottle will not be hollowed out, and the neck of the bottle will not be threaded.

import FreeCAD as App
import Part, math

def makeBottleTut(myWidth = 50.0, myHeight = 70.0, myThickness = 30.0):
    aPnt1=App.Vector(-myWidth / 2., 0, 0)
    aPnt2=App.Vector(-myWidth / 2., -myThickness / 4., 0)
    aPnt3=App.Vector(0, -myThickness / 2., 0)
    aPnt4=App.Vector(myWidth / 2., -myThickness / 4., 0)
    aPnt5=App.Vector(myWidth / 2., 0, 0)

    aArcOfCircle = Part.Arc(aPnt2, aPnt3, aPnt4)
    aSegment1=Part.LineSegment(aPnt1, aPnt2)
    aSegment2=Part.LineSegment(aPnt4, aPnt5)

    aEdge1=aSegment1.toShape()
    aEdge2=aArcOfCircle.toShape()
    aEdge3=aSegment2.toShape()
    aWire=Part.Wire([aEdge1, aEdge2, aEdge3])

    aTrsf=App.Matrix()
    aTrsf.rotateZ(math.pi) # rotate around the z-axis

    aMirroredWire=aWire.copy()
    aMirroredWire.transformShape(aTrsf)
    myWireProfile=Part.Wire([aWire, aMirroredWire])

    myFaceProfile=Part.Face(myWireProfile)
    aPrismVec=App.Vector(0, 0, myHeight)
    myBody=myFaceProfile.extrude(aPrismVec)

    myBody=myBody.makeFillet(myThickness / 12.0, myBody.Edges)

    neckLocation=App.Vector(0, 0, myHeight)
    neckNormal=App.Vector(0, 0, 1)

    myNeckRadius = myThickness / 4.
    myNeckHeight = myHeight / 10.
    myNeck = Part.makeCylinder(myNeckRadius, myNeckHeight, neckLocation, neckNormal)
    myBody = myBody.fuse(myNeck)

    return myBody

el = makeBottleTut()
Part.show(el)

Explicații detaliate

import FreeCAD as App
import Part, math

Vom avea, desigur, modulul Part, dar și modulul FreeCAD.Base, care conține structuri de bază FreeCAD precum vectori și matrice.

def makeBottleTut(myWidth = 50.0, myHeight = 70.0, myThickness = 30.0):
    aPnt1=App.Vector(-myWidth / 2., 0, 0)
    aPnt2=App.Vector(-myWidth / 2., -myThickness / 4., 0)
    aPnt3=App.Vector(0, -myThickness / 2., 0)
    aPnt4=App.Vector(myWidth / 2., -myThickness / 4., 0)
    aPnt5=App.Vector(myWidth / 2., 0, 0)

Aici definim funcția makeBottle. Această funcție poate fi apelată fără argumente, așa cum am făcut mai sus, caz în care valorile implicite pentru lățime, înălțime, și grosime vor fi utilizate. Apoi, definim câteva puncte care vor fi utilizate pentru construirea profilului de bază.

...
    aArcOfCircle = Part.Arc(aPnt2, aPnt3, aPnt4)
    aSegment1=Part.LineSegment(aPnt1, aPnt2)
    aSegment2=Part.LineSegment(aPnt4, aPnt5)

Aici definim geometria: un arc, format din 3 puncte și două segmente de linie, formate din câte 2 puncte.

...
    aEdge1=aSegment1.toShape()
    aEdge2=aArcOfCircle.toShape()
    aEdge3=aSegment2.toShape()
    aWire=Part.Wire([aEdge1, aEdge2, aEdge3])

Vă amintiți diferența dintre geometrie și forme? Aici construim forme geometrice ale construcției noastre. 3 margini (marginile pot fi drepte sau curbate), apoi o poliline realizează acele trei margini.

...
    aTrsf=App.Matrix()
    aTrsf.rotateZ(math.pi) # rotate around the z-axis

    aMirroredWire=aWire.copy()
    aMirroredWire.transformShape(aTrsf)
    myWireProfile=Part.Wire([aWire, aMirroredWire])

Până acum am construit doar o jumătate de profil. Mai ușor decât construirea întregului profil în același mod, putem doar să simetrizăm ceea ce am făcut și să lipim ambele jumătăți împreună. Așadar, vom crea mai întâi o matrice. O matrice este o modalitate foarte comună de a aplica transformări la obiecte din lumea 3D, deoarece poate conține într-o singură structură toate transformările de bază pe care obiectele 3D le pot suferi (mișcare, rotire și scalare). Aici, după ce creăm matricea, o oglindim și creăm o copie a poliliniei noastre cu matricea de transformare aplicată. Acum avem două polilinii și putem face o a treia polilinie din ele, deoarece poliliniile sun nt de fapt liste de margini.

...
    myFaceProfile=Part.Face(myWireProfile)
    aPrismVec=App.Vector(0, 0, myHeight)
    myBody=myFaceProfile.extrude(aPrismVec)

    myBody=myBody.makeFillet(myThickness / 12.0, myBody.Edges)

Acum că avem o polilinie închisă, aceasta poate fi transformat într-o fațetă. Odată ce avem o fațetă, o putem extruda. În acest fel, am făcut de fapt un solid. Apoi aplicăm o mică și frumoasă (pilire) rotunjire la obiectul nostru pentru că ne pasă de un design bun, nu-i așa?

...
    neckLocation=App.Vector(0, 0, myHeight)
    neckNormal=App.Vector(0, 0, 1)

    myNeckRadius = myThickness / 4.
    myNeckHeight = myHeight / 10.
    myNeck = Part.makeCylinder(myNeckRadius, myNeckHeight, neckLocation, neckNormal)

Apoi, corpul sticlei noastre este făcută, mai avem nevoie să creăm un gât. Deci noi face un nou solid, cu un cilindru.

...
    myBody = myBody.fuse(myNeck)

Funcționarea siguranței, care în alte aplicații este uneori numită uniune, este foarte puternică. Va avea grijă de lipirea a ceea ce trebuie lipit și de a elimina părțile care trebuie să fie eliminate.

...
    return myBody

Apoi, ne întoarcem Piesa noastră solidă ca rezultat al funcției noastre.

el = makeBottleTut()
Part.show(el)

În final, numim funcția definită și facem piesa vizibilă.

Paralelipiped găurit

Aici este un exemplul de construcție a unui paralelipiped găurit.

Here is a complete example of building a pierced box.

Construcția este realizată dintr-un capăt în altul iar când paralelipipedul este terminat, acesta este găurit cu un cilindru.

import FreeCAD as App
import Part, math

size = 10
poly = Part.makePolygon([(0, 0, 0), (size, 0, 0), (size, 0, size), (0, 0, size), (0, 0, 0)])

face1 = Part.Face(poly)
face2 = Part.Face(poly)
face3 = Part.Face(poly)
face4 = Part.Face(poly)
face5 = Part.Face(poly)
face6 = Part.Face(poly)
     
myMat = App.Matrix()

myMat.rotateZ(math.pi / 2)
face2.transformShape(myMat)
face2.translate(App.Vector(size, 0, 0))

myMat.rotateZ(math.pi / 2)
face3.transformShape(myMat)
face3.translate(App.Vector(size, size, 0))

myMat.rotateZ(math.pi / 2)
face4.transformShape(myMat)
face4.translate(App.Vector(0, size, 0))

myMat = App.Matrix()

myMat.rotateX(-math.pi / 2)
face5.transformShape(myMat)

face6.transformShape(myMat)               
face6.translate(App.Vector(0, 0, size))

myShell = Part.makeShell([face1, face2, face3, face4, face5, face6])   
mySolid = Part.makeSolid(myShell)

myCyl = Part.makeCylinder(2, 20)
myCyl.translate(App.Vector(size / 2, size / 2, 0))

cut_part = mySolid.cut(myCyl)

Part.show(cut_part)

Încărcare și salvare

Există mai multe moduri de a vă salva munca în modulul Part. Puteți bineînțeles salvați documentul FreeCAD, dar puteți salva și un obiect piesă/Part direct la formatele CAD obișnuite, cum ar fi BREP, IGS, STEP și STL.

There are several ways to save your work. You can of course save your FreeCAD document, but you can also save Part objects directly to common CAD formats, such as BREP, IGS, STEP and STL.

Salvarea unei forme într-un fișier este ușoară. Există metode disponibile exportBrep(), exportIges(), exportStl() și exportStep() pentru toate obiectele de formă. Deci, faci:

import Part
s = Part.makeBox(10, 10, 10)
s.exportStep("test.stp")

acest lucru va salva caseta noastră într-un fișier STEP. Pentru a încărca un BREP, IGES sau STEP, pur și simplu faceți contrariul:

import Part
s = Part.Shape()
s.read("test.stp")

Pentru a converti un fișier .stp în .igs este simplu :

import Part
 s = Part.Shape()
 s.read("file.stp")       # incoming file igs, stp, stl, brep
 s.exportIges("file.igs") # outbound file igs

Mesh Scripting

Mesh to Part

Power user documentation

FreeCAD scripting: Python, Introduction to Python, Python scripting tutorial, FreeCAD Scripting Basics

Modules: Builtin modules, Units, Quantity
Workbenches: Workbench creation, Gui Commands, Commands, Installing more workbenches
Meshes and Parts: Mesh Scripting, Topological data scripting, Mesh to Part, PythonOCC

Parametric objects: Scripted objects, Viewproviders (Custom icon in tree view)
Scenegraph: Coin (Inventor) scenegraph, Pivy
Graphical interface: Interface creation, Interface creation completely in Python (1, 2, 3, 4, 5), PySide, PySide examples beginner, intermediate, advanced
Macros: Macros, How to install macros
Embedding: Embedding FreeCAD, Embedding FreeCADGui

Other: Expressions, Code snippets, Line drawing function, FreeCAD vector math library (deprecated)

Hubs: User hub, Power users hub, Developer hub