Mesh Generation/de

Netze sind eine Möglichkeit, 3D-Formen als eine Reihe von Grundflächen zu modellieren, die durch Kanten und Punkte begrenzt sind. In der Regel handelt es sich dabei nicht um die Standarddarstellung von Formen in 3D-CAD-Programmen, da sie keine exakte Geometrie in Form von parametrischen Kurven und Flächen modellieren kann (solche Darstellungen werden als Boundary representation, B-rep, oder Begrenzungsflächenmodell bezeichnet). Dennoch hat ihre Einfachheit (zur Darstellung einer Form werden nur Punkte, Liniensegmente und einfache Flächen verwendet) Netze zur bevorzugten Darstellung für viele Anwendungen wie Rendering, Slicing für den 3D-Druck usw. gemacht. Wir haben bewusst die Verwendung von Netzen für FEM-Analysen (Finite-Elemente-Methode) nicht erwähnt, da Netze in diesem Fall nicht mehr wegen ihrer Einfachheit verwendet werden, sondern wegen ihrer Fähigkeit, Informationen durch Körper zu transportieren und zu verbreiten.

Die meisten parametrischen CAD-Modellierungsprogramme bieten Möglichkeiten zur Netzgenerierung und -bearbeitung, und FreeCAD bildet da keine Ausnahme. FreeCAD beherbergt eine Arbeitsbereich, spezialisiert auf die Arbeit mit Netzen das viele nützliche Werkzeuge und Funktionen bietet, und wir werden uns auf das konzentrieren, mit dem sich aus FreeCAD-Formen Netze generieren lassen: Mesh NetzAusPartForm.

Das Werkzeug ermöglicht die Verwendung von vier verschiedenen Vernetzungsalgorithmen: Standard, GMSH, NetGen und Mefisto. Wir konzentrieren uns auf den ersten, da die drei anderen für FEM-Analyse-Netze vorgesehen sind und nicht intern verwendet werden.

Der Standard-Algorithmus

Das Ziel dieser Seite ist es, einen Einblick in die Funktionsweise und Einrichtung von Netzwerken aus einer übergeordneten Perspektive zu geben, ohne dabei auf die komplexen Vorgänge bei der Netzgenerierung einzugehen. Der Standardalgorithmus steht für den Netzalgorithmus von OCCT, dem geometrischen Modellierungskern von FreeCAD. Dieser Algorithmus generiert unstrukturierte Oberflächennetze und funktioniert im Wesentlichen in zwei Schritten:

1. Die Kanten der Formen werden zunächst diskretisiert, d. h. Kurven werden in Polylinien umgewandelt (geschlossene Konturen werden somit zu Polygonen).
2. Anschließend werden die Oberflächen tesselliert, d. h. sie werden mit geometrischen Formen bedeckt, in unserem Fall mit Dreiecken.

Das Erzeugen eines Netzes aus einer Form ist ein komplexer Vorgang, der versteckte Aktionen und Parameter beinhaltet, die zu Verhaltensweisen führen können, die nicht trivial zu verstehen sind, insbesondere hinsichtlich der Einstellung der drei Parameter, auf die wir Zugriff haben. Schauen wir uns ihren Einfluss anhand praktischer Beispiele an, um besser zu verstehen, wie man gute Einstellungen definiert und schließlich gute Netze erzeugt.

Winkelabweichung

Die Winkelabweichung wird hauptsächlich beim Schritt der Kantendiskretisierung verwendet. Dieser Parameter trägt dazu bei, die Glätte von Polylinien, die Kurven darstellen, sicherzustellen, indem er scharfe Winkel zwischen aufeinanderfolgenden Liniensegmenten verhindert. Die Kantendiskretisierung hat einen großen Einfluss auf die gesamte Vernetzung der Formen, da die in diesem Schritt erzeugten Punkte (am Übergang zwischen Liniensegmenten) als Basisknoten für die Konstruktion von Dreiecken dienen, die wiederum zur Tessellierung der durch die Kanten begrenzten Flächen verwendet werden.

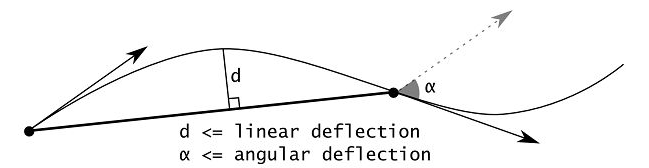
Dieser Parameterwert ist relativ zur Größe der zu vernetzten Form: Unabhängig von der Größe der Form kann ein hoher Winkelwert zu scharfen Übergängen zwischen aufeinanderfolgenden Liniensegmenten führen, während ein niedriger Wert für glattere Übergänge sorgt.

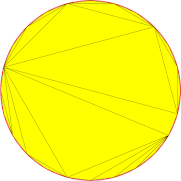
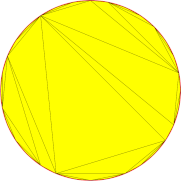
Um das Verhalten des Standardalgorithmus hinsichtlich der Winkelabweichung zu veranschaulichen, variieren wir diesen Parameter beim Vernetzen einer einfachen kreisförmigen Oberfläche. Da auch der Oberflächenabweichungsparameter eine Rolle in diesem Prozess spielt, wurde er auf einen Wert gesetzt, der hoch genug ist, um jegliche Beeinträchtigung unserer Demonstration zu vermeiden: Der Durchmesser unseres Kreises beträgt 50 mm, ebenso wie die Oberflächenabweichung.

Oben: Original BRep kreisförmige Fläche (blau), begrenzt durch den Außenkreis (rot) Unten: Detail oben links	Oberflächenabweichung: 50mm Winkelabweichung: 90°	Oberflächenabweichung: 50 mm Winkelabweichung: 30°	Oberflächenabweichung: 50 mm Winkelabweichung: 5°

Die Reduzierung der Winkelabweichung hat einen erheblichen Einfluss auf das Erscheinungsbild des Netzes, da sie scharfe Winkel bei der Darstellung der Gesichtskontur begrenzt. Sie ermöglicht zwar eine höhere Genauigkeit des Netzes im Verhältnis zur ursprünglichen Form, liefert jedoch keinen absoluten Wert für die maximal zulässige Abweichung zwischen beiden.

Oberflächenabweichung

Dazu ist die Option Oberflächenabweichung besser geeignet. Damit lässt sich die maximale Abweichung festlegen, die das Netz gegenüber der ursprünglichen Form aufweisen darf. Kehren wir zu unserer kreisförmigen Oberfläche zurück, um deren Einfluss zu verstehen.

Oberflächenabweichung: 50mm Winkelabweichung: 90°	Oberflächenabweichung: 10 mm Winkelabweichung: 90°	Oberflächenabweichung: 1 mm Winkelabweichung: 90°	Oberflächenabweichung: 0,1 mm Winkelabweichung: 90°

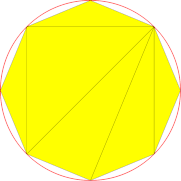
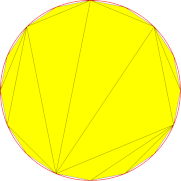
Der Einfluss der Oberflächenabweichung ist in unserem Beispiel aufgrund seiner absoluten Natur deutlich sichtbar und leicht verständlich. Er ist besonders nahe am Rand sichtbar: Hohe Werte (50 mm – 10 mm) haben keine Auswirkungen, während viele Dreiecke hinzugefügt werden, um die Toleranz von 0,1 mm sicherzustellen.

Kombinierter Einfluss von Winkel- und Oberflächenabweichung

Die Verringerung entweder der Winkelabweichung oder der Oberflächenabweichung hat ähnliche Auswirkungen auf das Netz. Diese Redundanz kann bei Verwendung ungünstiger Parameterkombinationen zu unerwünschtem Verhalten führen: Das folgende Beispiel zeigt die Erzeugung unnötiger, seltsam geformter Dreiecke, wenn sowohl die Winkel- als auch die Oberflächenabweichung auf niedrige Werte eingestellt sind.

Oberflächenabweichung: 10mm Winkelabweichung: 30°	Oberflächenabweichung: 3 mm Winkelabweichung: 7°	Oberflächenabweichung: 1 mm Winkelabweichung: 5°	Oberflächenabweichung: 0,1 mm Winkelabweichung: 1°

Erste Synthese

Die obigen Beispiele zeigen, dass es mithilfe von Winkel- und Oberflächenabweichung möglich ist, Netze innerhalb der geforderten Toleranz der ursprünglichen Form zu erhalten und die gewünschte Glätte bei der Darstellung von Kurven zu erreichen. Sie zeigen auch, wie wichtig eine angemessene Einstellung ist und dass die einfache Einstellung niedriger Werte möglicherweise nicht zu den besten Netzen führt.

Der Teufel steckt im Detail

Unsere Kreisform ermöglichte zwar ein gutes Verständnis des Einflusses der Parameter auf die Netzgenerierung, ist jedoch im Vergleich zu realen Herausforderungen bei der Netzgenerierung leider zu vereinfacht. Ein häufiger Fall ist das Vorhandensein feiner Details auf größeren Formen. Fügen wir unserer Kreisform ein Detail hinzu: eine kleinere kreisförmige Kante an der Oberseite.

Winkelabweichung / Oberflächenabweichung	90°	30°	5°
5mm
Anzahl Dreicke	10	32	149
1mm
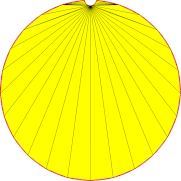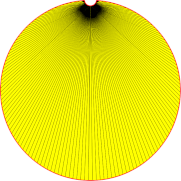Anzahl Dreicke	18	34	188
0.1mm
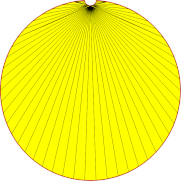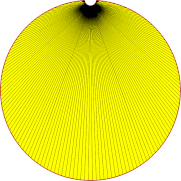Anzahl Dreicke	53	59	207

Winkelabweichung / Oberflächenabweichung	90°	30°	5°
5mm
Anzahl Dreiecke	10	32	149
1mm
Anzahl Dreiecke	18	34	188
0.1mm
Anzahl Dreiecke	53	59	207

Eine Verringerung der Winkelabweichung führt zu einer schnellen Erhöhung der Genauigkeit zwischen dem Netz und der ursprünglichen Form. Dies geht jedoch zu Lasten einer rapide steigenden Anzahl von Dreiecken. Andererseits ermöglicht eine Verringerung der Oberflächenabweichung die Erzeugung von Netzen, die genau die gewünschte Toleranz erfüllen, mit so vielen Dreiecken wie nötig, wobei jedoch die Glätte der Kurvendarstellung möglicherweise grob ist.

Auch hier lässt sich wieder die Redundanz zwischen den jeweiligen Einflüssen der Winkel- und Oberflächenabweichung feststellen, sowie eine gewisse Konvergenz hinsichtlich der Netzgenauigkeit, selbst wenn mehr Dreiecke hinzugefügt werden, insbesondere bei Verringerung der Winkelabweichung. Dies unterstreicht erneut, dass es besser ist, eine gute Einstellung zu finden, als einfach einen niedrigen Parameterwert zu wählen.

Beispiel für einen versteckten Parameter

Hohe Werte für Oberflächen- und Winkelabweichungen führen bei der Netzmodellierung nicht zur Unterdrückung von Details an der Oberseite unserer Form. Dies ist ein Beispiel für die Auswirkungen versteckter Operationen und Parameter innerhalb der Netzalgorithmen: Bestimmte Arten von Kanten, darunter auch kreisförmige Kanten, haben eine untere Grenze für die Anzahl der Punkte, die für ihre Polyliniendarstellung verwendet werden können. In diesem Fall führt das Minimum von 4 Punkten zu mindestens drei Segmenten innerhalb der Polylinie. Dies lässt sich durch die Vernetzung einer ähnlichen Form verdeutlichen, bei der jedoch anstelle einer kreisförmigen Kurve eine Spline verwendet wurde, um das Detail an der Oberseite zu modellieren. Die minimale Anzahl von Punkten gilt dann nicht, und das Detail wird bei hohen Werten der Oberflächenabweichung vollständig unterdrückt.

Geometrische Beschaffenheit des Details	Die Form	Das Netz	Eine Nahaufnahme
Arc of circle
Spline curve

Zweite Synthese

Diese Beispiele, einschließlich Details innerhalb größerer Formen, die im realen Leben sehr häufig vorkommen, zeigen, dass die Anpassung der Diskretisierungsgenauigkeit an die Größe der zu vernetzten Objekte zu einem besseren Kompromiss zwischen Netzgenauigkeit und Komplexität führen kann. Manchmal kann dies sogar zwingend erforderlich sein, beispielsweise bei automatisierten Vernetzungsvorgängen, bei denen der Benutzer nicht eingreifen kann, um die Oberflächenabweichung basierend auf der Formgröße festzulegen.

Relative Oberflächenabweichung

Eine Lösung besteht darin, die Oberflächenabweichung als Funktion der Kantenlänge festzulegen, was mithilfe des relativen Oberflächenabweichungsparameters erreicht wird. Das Prinzip besteht darin, die zulässige Toleranz zwischen dem Netz und der ursprünglichen Form als Funktion der Größe der Form zu skalieren. Ein Wert von 0,1 führt beispielsweise zu einer Oberflächenabweichung von 10 cm bei einer Kante von 1 m und zu einer Oberflächenabweichung von 1 m bei einer Kante von 10 m. Sehen wir uns die Ergebnisse an unserer Testform an.

Oberflächenabweichung (relativ) & Winkelabweichung	Das Netz	Eine Nahaufnahme	Eine genauere Betrachtung
0.1 - 30°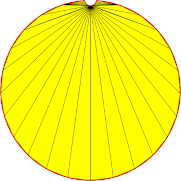
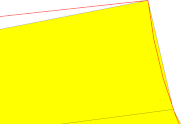0.001 - 30°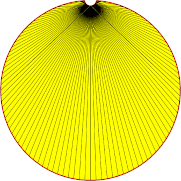

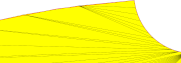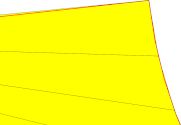Die Entwicklung des Oberflächenabweichungsparameters (der nun ein relativer Parameter ist, sodass die Einheit ´mm´ bei der Einstellung in FreeCAD verwirrend sein kann) gilt gleichermaßen für die Diskretisierung der langen und kurzen Kanten. Der Nebeneffekt der Verwendung der relativen Oberflächenabweichung besteht darin, dass sie keine absolute maximale Abweichung zwischen dem Netz und der ursprünglichen Form garantiert.

Oberflächen-Mosaikbildung

Unsere ersten Überlegungen konzentrierten sich auf Formen und Konturen, da diese als erste diskretisiert werden und einen erheblichen Einfluss auf die Gesichtsvernetzung haben. Lassen Sie uns etwas tiefer in die Oberflächenteilung mit dem Standardalgorithmus eintauchen. Dabei wird die Delaunay-Triangulation unter Verwendung des Watson-Algorithmus angewendet. Die Delaunay-Triangulation (benannt nach einem russischen Mathematiker) ist eine Methode zur Erzeugung von Punkten auf einer Oberfläche, die sicherstellt, dass sich die mit diesen Punkten gebildeten Dreiecke nicht überschneiden.

Darüber hinaus optimiert es die Dreiecksgenerierung, sodass die Winkel nicht zu klein sind und die Dreiecke gut geformt aussehen. Allerdings ist die praktische Umsetzung zur Lösung realer Probleme oft komplex und mit vielen Herausforderungen verbunden. Die OCCT-Meshing-Algorithmen wurden für die Vernetzung von Formen entwickelt, die mit dem BRep-Modellierer erstellt wurden, meist mechanische und technische Konstruktionen, für die der Geometrie-Modellierer ursprünglich entwickelt wurde.

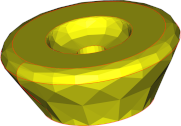
Daher werden spezielle Oberflächen-Tessellierungsroutinen für die gängigsten Oberflächentypen im Maschinenbau verwendet, z. B. planare, zylindrische, konische, sphärische Oberflächen usw., um Leistung und optimale Tessellierung zu gewährleisten. Wenn die Parametereinstellungen alle Oberflächentypen betreffen, untersuchen wir ihren Einfluss auf die B-Spline-Oberflächentessellierung, um Verzerrungen durch vorab festgelegte Tessellierungsstrategien zu vermeiden.

[[File:3D_orig_vignette.png	none|alt=Eine BRep-Form mit BSpline-Oberflächen|Eine BRep-Form mit BSpline-Oberflächen]]

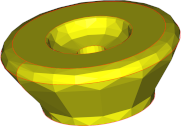
Winkelabweichung / Oberflächenabweichung	90°	30°	5°
5mm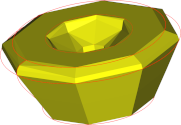
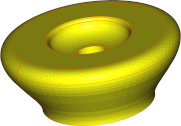Anzahl Dreiecke	196	666	9730
1mm
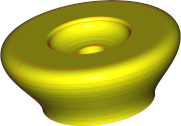Anzahl Dreiecke	376	790	26128
0.1mm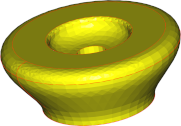
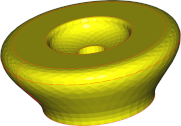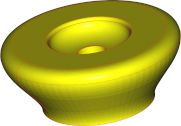Anzahl Dreiecke	3002	3262	36366

Die Schlussfolgerungen stimmen mit unseren Beobachtungen bei Flächen überein: Winkelabweichungen haben einen erheblichen Einfluss auf das Aussehen des Netzes, während Oberflächenabweichungen ein hohes Maß an Genauigkeit bei geringsten Kosten hinsichtlich der Komplexität des Netzes gewährleisten, jedoch sichtbare Facetten erzeugen. Somit muss ein Kompromiss zwischen der Qualität des Netzes hinsichtlich Genauigkeit und Glätte und der Größe des Netzes hinsichtlich der Anzahl der Dreiecke gefunden werden.

Wenn man neugierig ist, wie sich die Erhöhung der Anzahl der Dreiecke auswirkt, kann man sich einen Eindruck verschaffen, indem man mit dem Parameter Minimale Winkelabweichung der bevorzugten Software (Bearbeiten → Einstellungen → Part/Part Design → Formansicht) experimentiert, der die Genauigkeit der für die Visualisierung verwendeten Netze definiert. Ein zu niedriger Wert führt zu längeren Ladezeiten und ruckartigen Bewegungen bei komplexen Formen.

Eine weitere Möglichkeit, die Auswirkungen der Parameter zu erkennen, besteht darin, unsere Netze durch 3D-Druck in reale Objekte umzuwandeln. Der Harzdruck (SLA) mit einer Schichtdicke von 0,05 mm macht einige Details sichtbar.

Oberflächenabweichung & Winkelabweichung	0.1mm - 90°	5mm - 5°	0.1mm - 5°
Oberflächenbild
Oberflächenbild
Anzahl Dreiecke	3002	9730	36366

Diese Nahaufnahmen zeigen, dass die ausschließliche Konzentration auf Oberflächenabweichungen, selbst bei niedrigen Werten, zu sichtbaren Artefakten auf der Oberfläche des Teils führen kann (da der Zoomfaktor hoch ist, dürfen die Auswirkungen der Vernetzung nicht mit den Druckschichten verwechselt werden, die ebenfalls als Isolinien auf den Bildern sichtbar sind). Es ist schwierig, das 9730-Dreiecksnetz vom 36366-Dreiecksnetz hinsichtlich der visuellen Qualität zu unterscheiden. Wenn dies das Kriterium ist, sollte das leichtere Netz (487 KB gegenüber 1,8 MB) bevorzugt werden, da das andere die Gewähr bietet, dass die Toleranz von 0,1 mm überall im Teil eingehalten wird.

Letzte Synthese

Als Synthese sind Vernetzungsalgorithmen von Natur aus komplex, und Winkelabweichung und Oberflächenabweichung wirken auf komplexe Weise zusammen, die nicht trivial zu verstehen ist. Man könnte versucht sein, diese Parameter zu verringern, damit sich das Netz nahtlos an die ursprüngliche BRep-Form anpasst. Dies würde zu Netzen aus vielen Dreiecken führen, deren Erstellung und Verarbeitung in weiteren Anwendungen zeitaufwändig ist und die zu großen Dateien führen.

Arbeitsabläufe zur Parametereinrichtung

Nach unseren Beobachtungen besteht ein typischer Arbeitsablauf zur Festlegung der Parameter darin, zunächst die Oberflächenabweichung als Funktion der erforderlichen Genauigkeit zwischen dem Netz und der ursprünglichen Form festzulegen, sofern vorhanden. Anschließend kann der Parameter für die Winkelabweichung verwendet werden, um die Glätte der diskretisierten Oberflächen auf das erforderliche Niveau anzupassen, beispielsweise für visuelle oder haptische Aspekte. Ein anderer Ansatz besteht darin, eine ausreichend geringe Winkelabweichung zu verwenden, um die gewünschte Glätte zu erreichen, ohne dass eine absolute geometrische Toleranz garantiert ist, was oft auf Kosten komplexer Netze geht. In Fällen, in denen keine Toleranz hinsichtlich der Genauigkeit erforderlich ist, besteht eine weitere Option darin, die relative Oberflächenabweichung zu verwenden, wodurch die Größe der Netzelemente an die ursprüngliche Form und die Größe der Details angepasst wird.

Festlegen der Netzkonfiguration als FreeCAD-Standard

Wie im Abschnitt Einstellungen des Funktions-Wikis erläutert, kann man die bevorzugten Werte für Oberflächenabweichung, Winkelabweichung und relative Oberflächenabweichung als Standard festlegen, sodass man die meisten der Formen ohne weiteres Nachdenken vernetzen kann!

Die Netze exportieren

Sobald die Netze mit den geeigneten Parametern generiert wurden, kann man sie schließlich mit Netz Exportieren in eine Datei im Format der Wahl aus den verschiedenen Optionen, die FreeCAD bietet exportieren!