FEM MeshGmshFromShape/de
|
|
| Menüeintrag |
|---|
| Netz → FEM-Netz aus Form - Gmsh |
| Arbeitsbereich |
| FEM |
| Standardtastenkürzel |
| Keiner |
| Eingeführt in Version |
| - |
| Siehe auch |
| FEM Tutorium |
| Gleichungslöser |
|---|
| Alle |
Beschreibung
Für eine Finite-Elemente-Analyse muss die Geometrie in ein FEM-Netz diskretisiert werden. Dieser Befehl verwendet die Software Gmsh (die auf dem System installiert sein muss) zum Erstellen des Netzes.
Abhängig vom Betriebssystem und dem Installationspaket kann Gmsh in FreeCAD enthalten sein oder auch nicht. Für weitere Informationen siehe FEM Installation.
Anwendung
- Die Form auswählen, die analysiert werden soll. Bei der Volumen-FEM muss es sich um einen Festkörper oder Compsolid (zusammengesetzten Festkörper) handeln. Ein Compsolid ist erforderlich, wenn dein Teil aus mehreren Materialien besteht. (Ein Compsolid kann mit dem Befehl BoolescheFragmente erstellt werden).
- Es gibt mehrere Möglichkeiten, den Befehl aufzurufen:
- Die Schaltfläche
FEM-Netz aus Form - Gmsh drücken.
- Den Menüeintrag Netz →
FEM-Netz aus Form - Gmsh auswählen.
- Die Schaltfläche
- Wahlweise minimale und maximale Elementgröße anpassen (Die vorgegebene Einstellung erstellt oft zu grobe Netze). Es kann auch die dimensionale Art (1D, 2D, 3D) eingestellt (wobei die Voreinstellung From shape meistens passt) sowie die Ordnung des Elements geändert werden.
- Die Schaltfläche Anwenden anklicken und warten, bis die Erstellung des Netzes abgeschlossen ist. eingeführt in 1.0: Wahlweise die Schaltfläche Abbrechen drücken, um das Vernetzen abzubrechen.
- Die Schaltfläche OK drücken, um die Aufgabe abschließen. Jetzt sollte sich ein neues FEMMeshGmsh-Objekt im aktiven Analysebehälter befinden. Oder die Schaltfläche Abbrechen drücken, um die Änderung oder die Erstellung des Netzobjekts abzubrechen.
Nachdem das Netz erstellt wurde, können seine Eigenschaften im Eigenschafteneditor angepasst werden. Nach dem Ändern einer Eigenschaft, muss der Gmsh-Dialog erneut geöffnet und die Schaltfläche Anwenden gedrückt werden (der Dialog kann geöffnet bleiben, während weitere Eigenschaften geändert werden).
Die Schaltfläche Gmsh-Version erlaubt es, Details zur aktuell benutzten Gmsh-Binary zu überprüfen.
Eigenschaften
- Daten-EigenschaftAlgorithm2D: Der Algorithmus zum Erstellen von 2D-Netzen. Die verschiedenen Algorithmen werden hier erläutert. Für Delaunay siehe Delaunay-Triangulierung.
- Daten-EigenschaftAlgorithm3D: Der Algorithmus zum Erstellen von 3D-Netzen. Die verschiedenen Algorithmen werden hier erläutert.
- Daten-EigenschaftCharacteristic Length Max: Die maximale Größe der Netzelemente. Bei Einstellung auf 0.0 wird die Größe automatisch festgelegt. Diese Eigenschaft kann auch im Gmsh-Dialogfeld im Feld Max element size geändert werden.
- Daten-EigenschaftCharacteristic Length Min: Die minimale Größe der Netzelemente. Bei Einstellung auf 0.0 wird die Größe automatisch festgelegt. Diese Eigenschaft kann auch im Gmsh-Dialogfeld im Feld Min element size geändert werden.
- Daten-EigenschaftCoherence Mesh:
- true (Standard); doppelte Netzknoten werden entfernt.
- false
- Daten-EigenschaftElement Dimension: Die Dimension der Netzelemente. Diese Eigenschaft kann auch im Gmsh-Dialogfeld im Feld Mesh element dimension geändert werden.
- From Shape (Standard); die Dimension wird anhand der Dimension des zu vernetzenden Objekts bestimmt.
- 1D
- 2D
- 3D
- Daten-EigenschaftElement Order: Die Netz-Elementreihenfolge. Diese Eigenschaft kann auch im Gmsh-Dialogfeld im Feld Mesh order geändert werden. eingeführt in 0.20
- 1.
- 2. (Standard)
Hinweis: Wenn der Löser Elmer verwendet wird, kann folgende Fehlermeldung auftreten: ERROR:: GetEdgeBasis: Can't handle but linear elements, sorry. Das bedeutet, dass die Löser-Gleichung keine Netze zweiter Ordnung verarbeiten kann. In diesem Fall entweder Netze 1. Ordnung verwenden oder auf der FreeCAD-Wiki-Seite nach der Löser-Gleichung suchen, um mögliche Optionen für die Verarbeitung von Netzen 2. Ordnung zu finden.
- Daten-EigenschaftGeometry Tolerance: Die geometrische Toleranz für die Anpassung des Netzes an die Objektkanten. Der Standardwert 0.0 bedeutet, dass der Standardwert von Gmsh (1e-8) verwendet wird.
- Daten-EigenschaftGroups Of Nodes: Für jede physikalische Netzgruppe werden alle Knoten und nicht nur die Elemente gespeichert. Physikalische Gruppen sind Sammlungen von Netzelementen (Punkte, Kurven, Flächen und Volumen). Sie werden durch ihre Dimension und durch ein Tag identifiziert. Beispielsweise wird ein Netz desselben Objektbereichs intern mit demselben Tag versehen. Somit bilden alle Flächen dieses Bereichs eine physikalische Gruppe.
- Daten-EigenschaftHigh Order Optimize: Ob und wie Netze mit Daten-EigenschaftElement Order = 2nd optimiert werden. Die Optimierung erfolgt durch eine Verformung der Elementgrenzen.
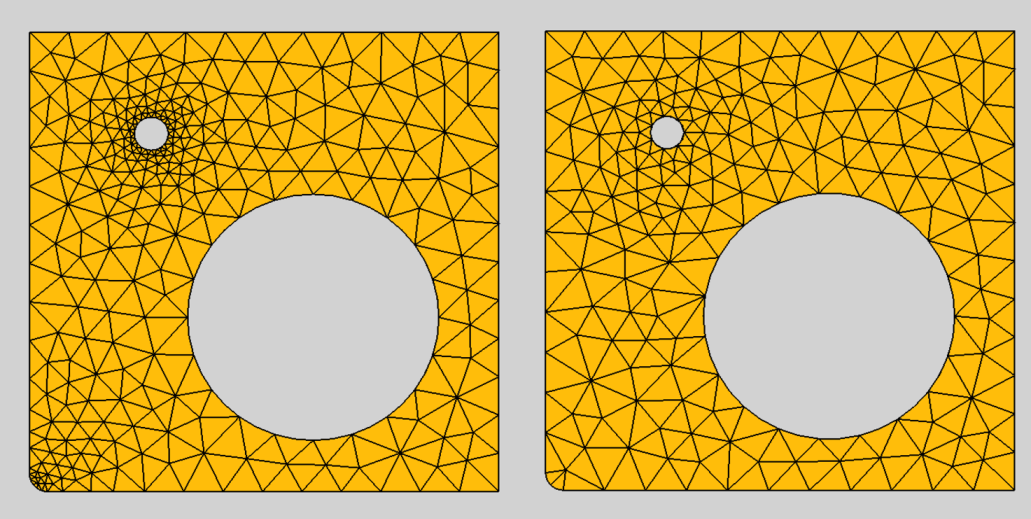
eingeführt in 0.20 Gmsh unterstützt verschiedene Optimierungsalgorithmen. Elastic (Elastisch) ist ein Algorithmus, bei dem die Netzelemente als eine Sammlung verformbarer viskoelastischer Festkörper behandelt werden. Netze erster Ordnung können nicht optimiert werden, da ihre Elementgrenzen linear sind und nicht verformt werden können. - Daten-EigenschaftMesh Size From Curvature eingeführt in 0.20: Die Anzahl der Netzelemente pro mal dem Radius der Krümmung. Um ein feineres Netz an kleinen Ecken oder Löchern zu erhalten, kann dieser Wert für bessere Ergebnisse erhöht werden.
Auswirkung von Mesh Size From Curvature; links: auf 12 gesetzt, rechts: deaktiviert
- Daten-EigenschaftOptimize Netgen: Gibt an, ob das Netz mit Hilfe des 3D-Netzgenerators Netgen optimiert wird, um die Qualität der Tetraederelemente zu verbessern. Hinweis: Da Netgen nur tetraedrische Elemente erstellen kann, wird diese Option für Netze ignoriert, deren Daten-EigenschaftElement Dimension nicht 3D ist.
- Daten-EigenschaftOptimize Std Optimiert das Netz, um die Qualität der tetraedrischen Elemente zu verbessern.
- Daten-EigenschaftRekombinationsalgorithmus eingeführt in 0.20: Der Algorithmus, der für Daten-EigenschaftRecombine 3D All und auch für Daten-EigenschaftRecombine All verwendet wird. Weitere Informationen findet man im Abschnitt Elementrekombination und technische Details in der Gmsh-Dokumentation.
- Daten-EigenschaftRecombine 3D All eingeführt in 0.20: Wendet einen 3D-Rekombinationsalgorithmus auf alle Volumen an. Tetraeder werden nach Möglichkeit zu Prismen, Hexaedern oder Pyramiden rekombiniert.
- Daten-EigenschaftRecombine All: Wendet einen Rekombinationsalgorithmus auf alle Oberflächen an. Dreiecke werden nach Möglichkeit zu Vierecken rekombiniert.
- Daten-EigenschaftSecond Order Linear: Option, wenn Knoten zweiter Ordnung (wenn Daten-EigenschaftElement Order auf 2nd gesetzt ist) und/oder Netzverfeinerungspunkte durch lineare Interpolation erstellt werden.
- true; lineare Interpolation wird verwendet.
- false (Standard); kurvenförmige Interpolation wird verwendet.
- Daten-EigenschaftSubdivision Algorithm eingeführt in 1.0: Ermöglicht die Erstellung von Viereck- und Hexaederelementen durch Unterteilung.
- Keine; verwendet keinen Unterteilungsalgorithmus
- Alle Vierecke; erstellt viereckige Elemente durch Unterteilung
- Alle Hexaeder; erstellt hexaedrische Elemente durch Unterteilung
- Baryzentrisch; erstellt dreieckige Elemente durch baryzentrische Unterteilung
Hinweise
Nichtpositive Jacobi-Matrizen
Wenn ein Vermaschungs-Fehler über Nichtpositive Jacobi-Matrizen auftritt, können die folgenden Lösungsstrategien angewendet werden:
- Setze Daten-EigenschaftSecond Order Linear auf true, aber belasse Daten-EigenschaftElement Order auf „2nd“.
- Setze Daten-EigenschaftElement Order auf 1st.
- Eine kleinere Elementgröße verwenden, indem man die Daten-EigenschaftCharacteristic Length Max reduziert.
- Wenn der Löser ccxtools verwendet wird und die Schaltfläche Ausführen (nicht das Aufgaben-Fenster) verwendet wird, werden die Knoten der nicht positiven Jacobi-Elemente grün dargestellt.
Netz-Wachstum
An Kanten und kleinen geometrischen Elementen muss das Netz kleiner sein als in Bereichen ohne Kanten. Daher nimmt die Größe der Netzelemente mit zunehmender Entfernung von den Kanten zu. Die Wachstumsstrategie von Gmsh besteht darin, zwischen Kanten unterschiedlicher Größe zu wachsen. Das Wachstum schlägt also fehl, wenn ein Bereich Kanten gleicher Größe aufweist, wie beispielsweise bei diesem Rohr:
Fehlgeschlagenes Netz-Wachstum, da der zylindrische Bereich von den gleichen Kanten umgeben ist
Um ein sinnvolles Netzwachstum zu ermöglichen, muss in diesem Fall dem Bereich eine Kante hinzugefügt werden. Im Beispiel wäre dies ein Kreis in der Mitte des Zylinders. Der Kreis wird als Teil eines Verbunds BoolescheBestandteile (um ein CompSolid zu bilden), siehe die Projekt-Datei für das Beispiel.
Sinnvolles Netzwachstum aufgrund der zusätzlichen Kante in der Mitte des zylindrischen Bereichs
Element-Rekombination
Elemente können auf zwei Arten neu kombiniert werden: auf der Oberfläche von Objekten, sodass Dreiecke nach Möglichkeit zu Vierecken neu kombiniert werden, und im Volumen von Objekten, sodass Tetraeder nach Möglichkeit zu Prismen, Hexaedern oder Pyramiden neu kombiniert werden. Betrachtet man die Geometrie, wird deutlich, dass das Ergebnis der Neukombination stark von der Geometrie des Körpers abhängt und dass die Neukombination eines 3D-Körpers nur an der Oberfläche meist zu seltsamen Ergebnissen führt.
Zur Veranschaulichung sehe man sich das Bild unten an. Ein Quaderkörper wird mit den Standardeinstellungen (Tetraeder, Netz der 2. Ordnung) vernetzt. Dies ist das Teilbild oben links. Das Bild oben rechts zeigt das Ergebnis, wenn zusätzlich die Elemente nur an der Oberfläche des Körpers neu kombiniert werden. Das Ergebnis ist schlecht, da die geänderten Oberflächenelemente nicht zu den unveränderten Volumenelementen passen. Daher ist Daten-EigenschaftRecombine All allein in der Regel nur für 2D-Netze sinnvoll.
Wenn wir jetzt auch Daten-EigenschaftRecombine 3D All verwenden, ist das Ergebnis besser, siehe das untere linke Teilbild. Allerdings zeigt das Ergebnis keinen großen Unterschied zu dem Netz ohne Rekombinationen. Da unser Körper ein Quader ist, ist es daher sinnvoll, einen Rekombinationsalgorithmus zu verwenden, der ebenfalls versucht, Quader zu erzeugen. Dieses Ergebnis ist im unteren rechten Teilbild zu sehen.
Der einfache Rekombinationsalgorithmus lässt einige Dreiecke im Netz zurück, falls die Rekombination zu schlecht geformten Vierecken führt. Man verwendet in solchen Fällen einen Full-Quad-Rekombinationsalgorithmus, der automatisch ein gröberes Netz erstellt, gefolgt von der Rekombination, Glättung und Unterteilung. Siehe Foren-Thema
Auswirkung der Rekombination von Netzelementen.
Oben links: Standardnetz.
Oben rechts: Rekombination nur an der Oberfläche unter Verwendung des einfachen Algorithmus.
Unten links: Rekombination an der Oberfläche und im Volumen unter Verwendung des einfachen Algorithmus.
Unten rechts: Rekombination an der Oberfläche und im Volumen unter Verwendung des einfachen full-quad Algorithmus
- Materials: Solid Material, Fluid Material, Non-Linear Mechanical Material, Reinforced Material (Concrete); Material Editor
- Element Geometry: Beam Cross Section, Beam Rotation, Shell Plate Thickness, Fluid Section for 1D Flow
- Electromagnetic Boundary Conditions: Electrostatic Potential Boundary Condition, Current Density Boundary Condition, Magnetization Boundary Condition, Electric Charge Density
- Fluid Boundary Conditions: Initial Flow Velocity Condition, Initial Pressure Condition, Flow Velocity Boundary Condition
- Geometrical Analysis Features: Plane Multi-Point Constraint, Section Print Feature, Local Coordinate System
- Mechanical Boundary Conditions and Loads: Fixed Boundary Condition, Rigid Body Constraint, Displacement Boundary Condition, Contact Constraint, Tie Constraint, Spring Boundary Condition, Force Load, Pressure Load, Centrifugal Load, Gravity Load
- Thermal Boundary Conditions and Loads: Initial Temperature, Heat Flux Load, Temperature Boundary Condition, Body Heat Source
- Overwrite Constants: Constant Vacuum Permittivity
- Mesh: Mesh From Shape by Netgen, Mesh From Shape by Gmsh, Mesh Boundary Layer, Mesh Refinement, Mesh Group, Erase Elements, FEM Mesh to Mesh
- Solve: Solver CalculiX, Solver Elmer, Solver Mystran, Solver Z88; Mechanical Equations: Elasticity Equation, Deformation Equation; Electromagnetic Equations: Electrostatic Equation, Electricforce Equation, Magnetodynamic Equation, Magnetodynamic 2D Equation, Static Current Equation; Flow Equation, Flux Equation, Heat Equation, Solver Job Control, Run Solver
- Results: Purge Results, Show Result, Apply Changes to Pipeline, Post Pipeline From Result, Pipeline Branch, Warp Filter, Scalar Clip Filter, Function Cut Filter, Region Clip Filter, Contours Filter, Glyph Filter, Line Clip Filter, Stress Linearization Plot, Data at Point Clip Filter, Calculator Filter; Filter Functions: Plane, Sphere, Cylinder, Box; Data Visualizations: Create Lineplot, Create Histogram, Create Table
- Utilities: Clipping Plane on Face, Remove All Clipping Planes, FEM Examples; Clear FEM Mesh, Display Mesh Info
- Additional: Preferences; FEM Install, FEM Mesh, FEM Solver, FEM CalculiX, FEM Concrete; FEM Element Types
- Erste Schritte
- Installation: Herunterladen, Windows, Linux, Mac, Zusätzliche Komponenten, Docker, AppImage, Ubuntu Snap
- Grundlagen: Über FreeCAD, Graphische Oberfläche, Mausbedienung, Auswahlmethoden, Objektname, Voreinstellungseditor, Arbeitsbereiche, Dokumentstruktur, Objekteigenschaften, FreeCAD unterstützen, Spenden
- Hilfe: Anleitungen, Videoanleitungen
- Arbeitsbereiche: Std Base, Arch, Assembly, BIM, CAM, Draft, FEM, Inspection, Material, Mesh, OpenSCAD, Part, PartDesign, Points, Reverse Engineering, Robot, Sketcher, Spreadsheet, Surface, TechDraw, Test Framework